题目内容
18.设数列{an}的前n项和为Sn,且Sn=n2+2n(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明{an}是等差数列.
分析 (Ⅰ)根据数列项和前n项和之间的关系即可求数列{an}的通项公式;
(Ⅱ)根据等差数列的定义进行证明即可.
解答 解:(Ⅰ)∵Sn=n2+2n,
∴a1=S1=3,
当n≥2时,an=Sn-Sn-1=n2+2n-[(n-1)2+2(n-1)]=2n+1,
则当n=1时,满足an=2n+1,综上都有an=2n+1.
(Ⅱ)∵an-an-=2(n+1)+1-2n-1=2,为常数,
∴{an}是首项为3,公差为2的等差数列.
点评 本题主要考查等差数列的通项公式的求解和证明,比较基础.

练习册系列答案
相关题目
6.已知定义域为R的函数f(x)满足f(x)=2f(2-x)-x2+8x-8,则曲线y=f(x)在点(2,f((2))处的切线方程是( )
| A. | 4x-y+4=0 | B. | 4x-y-4=0 | C. | 4x+y+4=0 | D. | 4x+y-4=0 |
3.由不等式组$\left\{\begin{array}{l}{1≤x≤e}\\{lnx-y+1≥0}\\{2x-(e-1)y-2≤0}\end{array}\right.$确定的平面区域为M,由不等式组$\left\{\begin{array}{l}{1≤x≤e}\\{0≤y≤2}\end{array}\right.$确定的平面区域为N,在N内随机的取一点P,则点P落在区域M内的概率为( )
| A. | $\frac{1}{2e-2}$ | B. | $\frac{e-2}{2e-2}$ | C. | $\frac{3-e}{4e-4}$ | D. | $\frac{e}{2e-2}$ |
7.已知f是有序数对集合M={(x,y)|x∈N*,y∈N*}上的一个映射,正整数数对(x,y)在映射f下对应的为实数z,记作f(x,y)=z.对于任意的正整数m,n(m>n),映射f由下表给出:
则使不等式f(2,x)≤3的解集为{1,2}.
| (x,y) | (n,n) | (m,n) | (n,m) |
| f(x,y) | n | m-n | m+n |
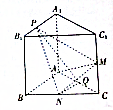 如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动.
如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动. 已知空间四边形OABC,如图所示,其对角线为OB,AC.M,N分别为OA,BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=2$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x+y+z=$\frac{5}{6}$.
已知空间四边形OABC,如图所示,其对角线为OB,AC.M,N分别为OA,BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=2$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x+y+z=$\frac{5}{6}$.