题目内容
在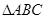 中,
中,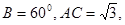 则AB+3BC的最大值为 .
则AB+3BC的最大值为 .
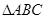 中,
中,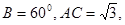 则AB+3BC的最大值为 .
则AB+3BC的最大值为 .
试题分析:∵B=60°,A+B+C=180°,∴A+C=120°,由正弦定理得
 ,∴AB=2sinC,BC=2sinA.∴AB+3BC=2sinC+6sinA=2sin(120°-A)+6sinA=2(sin120°cosA-cos120°sinA)+6sinA=
,∴AB=2sinC,BC=2sinA.∴AB+3BC=2sinC+6sinA=2sin(120°-A)+6sinA=2(sin120°cosA-cos120°sinA)+6sinA= cosA+7sinA=
cosA+7sinA= sin(A+φ),(其中tanφ=
sin(A+φ),(其中tanφ= ),所以AB+3BC的最大值为
),所以AB+3BC的最大值为 .
.点评:解题时要认真审题,注意正弦定理和三角函数恒等变换的合理运用

练习册系列答案
相关题目
 中,
中, ,则
,则


 或
或
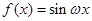
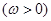 在区间
在区间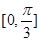 上单调递增,在区间
上单调递增,在区间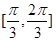 上单调递减;如图,四边形
上单调递减;如图,四边形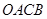 中,
中,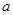 ,
,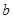 ,
,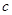 为
为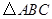 的内角
的内角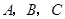 的对边,
的对边,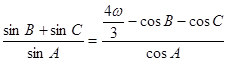 .
.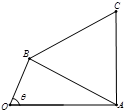
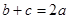 ;
;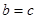 ,设
,设 ,
, ,
,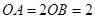 ,求四边形
,求四边形 ,b=12,
,b=12, ,则
,则 的值为__________.
的值为__________. =
= =
= ,则△ABC是
,则△ABC是 a,则
a,则 的值为
的值为
 中,
中, ,
, ,
, ,则
,则 =________.
=________. 分别是锐角
分别是锐角 的三边
的三边 、
、 、
、 所对的角,
所对的角, .
.  的大小;
的大小; 求
求 的最小值.
的最小值. ,A+C=2B,则sinC=
,A+C=2B,则sinC=