题目内容
已知函数y=f(x)的定义域为(0,+∞),f(x)的导函数为f(x),且对任意正数X均有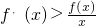 ,则下列结论中正确的是
,则下列结论中正确的是
- A..y=f(x)在(0,+∞)上为增函数
- B..y=
 在(0,+∞)上为减函数
在(0,+∞)上为减函数 - C.若x1,x2∈(0,+∞)则f((x1)+f(x2)>f(x1+x2)
- D.若x1,x2∈(0,+∞),则f(x1)+f(x2)<f(x1+x2)
D
分析:由于函数为抽象函数.所以此题只能从f(x)的导函数为f(x),且对任意正数X均有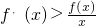 入题,得到
入题,得到 ,利用不等式的性质即可.
,利用不等式的性质即可.
解答:由f′(x)> ?
? >0,
>0,
又x>0?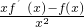 >0 即:
>0 即: >0?
>0? 在(0,+∞)上单调递增,
在(0,+∞)上单调递增,
又x1,x2∈(0,+∞)?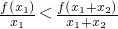
即:(x1+x2)f(x1)<x1f(x1+x2)①
同理:(x1+x2)f(x2)<x2f(x1+x2)②
①+②得:f(x1)+f(x2)<f(x1+x2).
故答案选D
点评:此题考查了利用导函数解决函数的单调性,还考查了不等式的性质.
分析:由于函数为抽象函数.所以此题只能从f(x)的导函数为f(x),且对任意正数X均有
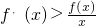 入题,得到
入题,得到 ,利用不等式的性质即可.
,利用不等式的性质即可.解答:由f′(x)>
 ?
? >0,
>0,又x>0?
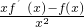 >0 即:
>0 即: >0?
>0? 在(0,+∞)上单调递增,
在(0,+∞)上单调递增,又x1,x2∈(0,+∞)?
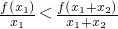
即:(x1+x2)f(x1)<x1f(x1+x2)①
同理:(x1+x2)f(x2)<x2f(x1+x2)②
①+②得:f(x1)+f(x2)<f(x1+x2).
故答案选D
点评:此题考查了利用导函数解决函数的单调性,还考查了不等式的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足