题目内容
 学校为了了解某学科模块测试情况,随机抽取了甲、乙两班各10名同学的成绩(满分100分),获得成绩数据的茎叶图如图:
学校为了了解某学科模块测试情况,随机抽取了甲、乙两班各10名同学的成绩(满分100分),获得成绩数据的茎叶图如图:(I)根据茎叶图判断哪个班的平均成绩较高;
(II)计算甲班的样本方差;
(III)现从乙班这10名同学中随机抽取两名成绩不低于83分的同学,求成绩为86分的同学被抽中的概率.
分析:(I)根据茎叶图所给的两个班的10名同学的成绩,做出两名同学的平均分,进行比较,得到甲班的平均数低于乙班的平均数.
(II)根据茎叶图所给的甲班的分数和甲班的平均数,代入方差公式,做出这组数据的方差,注意不要漏掉数据.
(III)本题是一个等可能事件的概率,试验发生包含的事件是从乙班10名同学中抽取两名成绩不低于83的可以通过列举得到结果数,满足条件的事件也可以通过列举得到结果数,求出概率.
(II)根据茎叶图所给的甲班的分数和甲班的平均数,代入方差公式,做出这组数据的方差,注意不要漏掉数据.
(III)本题是一个等可能事件的概率,试验发生包含的事件是从乙班10名同学中抽取两名成绩不低于83的可以通过列举得到结果数,满足条件的事件也可以通过列举得到结果数,求出概率.
解答:解:(I)由茎叶图可知:
=
=80
=
=81.1
∴
>
(II)甲班的样本方差:S2=
[(80-68)2+(80-78)2+(80-78)2+
(80-73)2+(80-72)2+(80-89)2+(80-89)2+(80-81)2
+(80-80)2+(80-92)2]=57.2
(III)由题意知本题是一个等可能事件的概率,
试验发生包含的事件是从乙班10名同学中抽取两名成绩不低于83的有:(91,83),(91,86),
(91,88),(91,89),(89,83),(89,86),(89,88),(88,83),
(88,86),(86,83)共有10个基本事件
设成绩为86的同学被抽中的事件A,则事件A所含(91,86),(89,86),
(88,86),(86,83)共4个基本事件
∴P(A)=
=
.
. |
| x甲 |
| 92+80+81+89+89+72+73+78+78+78+68 |
| 10 |
. |
| x乙 |
| 91+80+83+86+88+89+72+75+78+69 |
| 10 |
∴
. |
| x乙 |
. |
| x甲 |
(II)甲班的样本方差:S2=
| 1 |
| 10 |
(80-73)2+(80-72)2+(80-89)2+(80-89)2+(80-81)2
+(80-80)2+(80-92)2]=57.2
(III)由题意知本题是一个等可能事件的概率,
试验发生包含的事件是从乙班10名同学中抽取两名成绩不低于83的有:(91,83),(91,86),
(91,88),(91,89),(89,83),(89,86),(89,88),(88,83),
(88,86),(86,83)共有10个基本事件
设成绩为86的同学被抽中的事件A,则事件A所含(91,86),(89,86),
(88,86),(86,83)共4个基本事件
∴P(A)=
| 4 |
| 10 |
| 2 |
| 5 |
点评:本题考查茎叶图,考查两组数据的平均数,考查一组数据的方差,考查等可能事件的概率,是一个概率统计的综合题目.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
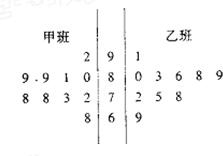 学校为了了解某学科模块测试情况,随机抽取了甲、乙两班各10名同学的成绩(满分100分),获得成绩数据的茎叶图如图:
学校为了了解某学科模块测试情况,随机抽取了甲、乙两班各10名同学的成绩(满分100分),获得成绩数据的茎叶图如图:

