题目内容
(本小题满分15分)
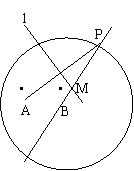
已知定点A、B间的距离为2，以B为圆心作半径为2
的圆，P为圆上一点，线段AP的垂直平分线l与直线PB交于点M，当P在圆周上运动时，点M的轨迹记为曲线C．
(1)建立适当的坐标系，求曲线C的方程，并说明它是什么样的曲线；
(2)试判断l与曲线C的位置关系，并加以证明．
解 (1)以AB中点为坐标原点，直线AB所在直线为x轴建立平面直角坐标系，则A(－1,0)，B(1,0).
设M(x, y),由题意：|MP|=|MA|, |BP|=2
，所以 |MB|+|MA|=2.
故曲线C是以A、B为焦点，长轴长为2的椭圆，其方程为x2+2y2=2.
(2)直线l与曲线C的位置关系是相切.
证法一：由(1)知曲线C方程为x2+2y2=2，
设P(m, n)，则P在⊙B上，故(m－1)2+n2=8， 即m2+n2=7+2m.
当P、A、B共线时，直线l的方程为x=±，显然结论成立.
当P、A、B不共线时，直线l的方程为：
,整理得，
把直线l的方程代入曲线C方程得：
，
整理得
∴直线l与曲线C相切.(说明：以A或B为原点建系亦可)
证法二：在直线l上任取一点
，连结
，由垂直平分线的性质得
，
∴
(当且仅当M、重合时取“=”号)
∴直线l与椭圆C有且仅有一个公共点M. 结论得证
练习册系列答案
同步练习强化拓展系列答案
相关题目
的单调区间；
，试分别解答以下两小题.
对任意的
恒成立，求实数
的取值范围；
是两个不相等的正数，且
，求证：
．
、
分别为椭圆
：
的 
：
的焦点，
是
。
：
，过点P的动直线
与圆
，
（
且
）。求证：点Q总在某定直线上。
的左、右焦点分别为
、
，过
与椭圆相交于A、B两点。
，且
，求椭圆的离心率；
求
的最大值和最小值。
在定义域内存在区间
，满足
是否为“优美函数”？若是，求出
；若不是，说明理由；
为“优美函数”，求实数
的取值范围．