题目内容
(2005•湖南)设函数f (x)的图象与直线x=a,x=b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积,已知函数y=sinnx在[0,
]上的面积为
(n∈N*),
(i)y=sin3x在[0,
]上的面积为
;
(ii)y=sin(3x-π)+1在[
,
]上的面积为
| π |
| n |
| 2 |
| n |
(i)y=sin3x在[0,
| 2π |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
(ii)y=sin(3x-π)+1在[
| π |
| 3 |
| 4π |
| 3 |
π+
| 2 |
| 3 |
π+
.| 2 |
| 3 |
分析:(i)函数y=sinnx与函数y=sin3x类比,可以得出函数y=sin3x在[0,
]上的面积,得出函数y=sin3x在[0,
]上的面积是函数y=sin3x在[0,
]上的面积的两倍,从而得出函数y=sin3x在[0,
]上的面积.
(ii)设t=x-
,t∈[0,π],则y=sin3t+1,同理可求.
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
(ii)设t=x-
| π |
| 3 |
解答:解:(i)∵函数y=sinnx在[0,
]上的面积为
((n∈N+),∴对于函数y=sin3x而言,n=3,
∴函数y=sin3x在[0,
]上的面积为:
,则函数y=sin3x在[0,
]上的面积为
×2=
(ii)设t=x-
,t∈[0,π],则y=sin3t+1,∴y=sin(3x-π)+1在[
,
]上的面积为π+
故答案为:
,π+
| π |
| n |
| 2 |
| n |
∴函数y=sin3x在[0,
| π |
| 3 |
| 2 |
| 3 |
| 2π |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
(ii)设t=x-
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
| 2 |
| 3 |
故答案为:
| 4 |
| 3 |
| 2 |
| 3 |
点评:在解题过程中,寻找解题的突破口,往往离不开类比联想,我们在解题中,要进一步通过概念类比、性质类比、结构类比以及方法类比等思维训练途径,来提高类比推理的能力,培养探究创新精神.

练习册系列答案
相关题目
(2005
湖南,10)设P是△ABC内任意一点,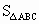 表示△ABC的面积,
表示△ABC的面积,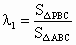 ,
,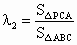 ,
,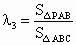 ,定义
,定义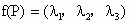 ,若G是△ABC的重心,
,若G是△ABC的重心, ,则
,则
[
]|
A .点Q在△GAB内 |
B .点Q在△GBC内 |
|
C .点Q在△GCA内 |
D .点Q与点G重合 |
 ,
, ,则
,则 ________.
________.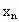 表示某鱼群在第n年年初的总量,
表示某鱼群在第n年年初的总量,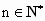 ,且
,且 ,不考虑其他因素,设在第n年内鱼群的繁殖量及被捕捞量都与
,不考虑其他因素,设在第n年内鱼群的繁殖量及被捕捞量都与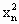 成正比,这些比例系数依次为正常数a、b、c.
成正比,这些比例系数依次为正常数a、b、c.
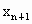 与
与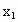 、a、b、c满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
、a、b、c满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
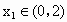 ,都有
,都有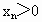 ,
,