Question

已知f（x）=ax²+bx+1
（1）若f（x）＞0的解集是（-1，2），求实数a，b的值；
（2）若f（-1）＞0且f（2）＞0，求3a-b的取值范围．

Answer 1

分析：（1）由一元二次方程的根与一元二次不等式的解集的关系即可求出a、b的值；
（2）由已知作出可行域，考虑目标函数t=3a-b，变形为b=3a-t，作出一族平行线，即可得出t的取值范围．

解答：解：（1）∵f（x）＞0的解集是（-1，2），∴-1，2是方程ax²+bx+1=0的两个实数根，且a＜0．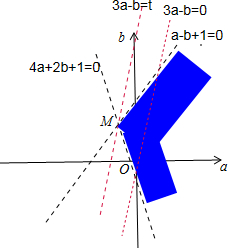
∴

f(-1)=a-b+1=0 f(2)=4a+2b+1=0 a＞0

，解得

a=- 1 2 b= 1 2

．
（2）由已知可得

f(-1)=a-b+1＞0 f(2)=4a+2b+1＞0

，作出可行域如图：
设3a-b=t，则b=3a-t，这是斜率为3、随t变化的一族平行直线．
可以看出当经过二直线a-b+1=0与4a+2b+1=0的交点(-

1

2

，

1

2

)时，在b轴上的截距最大，
∴-t＞

1

2

-3×(-

1

2

)=2，
∴t＜-2，即3a-b＜-2．

点评：掌握一元二次不等式的解集与相应的一元二次方程的根的关系及正确作出线性规划的可行域与目标函数的图象是解题的关键．