Question

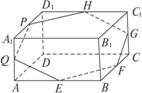
18.如下图,在长方体ABCD—A₁B₁C₁D₁中,已知AB=4,

AD=3,AA₁=2. E、F分别是线段AB、BC上的点,且EB=FB=1.

（Ⅰ）求二面角C—DE—C₁的正切值;

（Ⅱ）求直线EC₁与FD₁所成角的余弦值.

Answer 1

18.本小题主要考查二面角、异面直线所成的角、空间向量等知识和思维能力、空间想象能力、运算能力.

     解法一：（Ⅰ）过C作CG⊥DE，垂足为G，连结C₁G.

　　∵CC₁⊥平面ABCD，

　　∴CG是C₁G在平面ABCD上的射影，

　　由三垂线定理得DE⊥C₁G.

　　∴∠CGC₁是二面角C－DE－C₁的平面角.

　　在△ADE中，AE＝AD＝3，∠DAE＝90，

　　∴∠ADE＝45∠CDG＝90－45=45.

　　∴CG＝CD·sin∠CDG＝4×sin45=2.

    ∴tan∠CGC₁===.

　（Ⅱ）延长BA至点E₁，使AE₁＝1，连结E₁F、DE₁、D₁E₁、DF，

　　　　有D₁C₁∥E₁E，D₁C₁＝E₁E，则四边形D₁E₁EC₁是平行四边形.

　　　　所以E₁D₁∥EC₁.于是∠E₁D₁F为EC₁与FD₁所成的角.

　　　　在Rt△BE₁F中，E₁F＝＝＝.

　　　　在Rt△D₁DE₁中，D₁E₁＝＝　＝＝.

　　　　在Rt△D₁DF中，FD₁＝＝

＝＝.

    　　所以在△E₁FD₁中，由余弦定理得：

　      cosE₁D₁F＝==.

　　解法二：（Ⅰ）以A为原点,、、

分别为x轴、y轴、z轴的正向建立空间直角坐标系,则有

D（0,3,0）、D₁（0,3,2）、E（3,0,0）、F（4,1,0）、C₁（4,3,2）

于是,=（3,－3,0）,=（1,3,2）,=（－4,2,2）.

设向量n=（x,y,z）与平面C₁DE垂直,则有

x=y=－z.

∴n=（－,－,z）=（－1,－1,2）,其中z>0.

取n₀=（－1,－1,2）,则n₀是一个与平面C₁DE垂直的向量.

∵向量=（0,0,2）与平面CDE垂直,

∴n₀与所成的角θ为二面角C－DE－C₁的平面角.

∴cosθ===,

∴tanθ=.

（Ⅱ）设EC₁与FD₁所成角为β,则

cosβ===.