Question

（本小题满分12分）

如图，在四棱锥中，底面为菱形，，为的中点。

   （1）若，求证：平面平面；

   （2）点在线段上，，试确定的值，使平面；

   （3）在（2）的条件下，若平面平面ABCD，且，求二面角的大小。

Answer 1

解：（1）连BD，四边形ABCD菱形，  ∵AD⊥AB，  ∠BAD=60°

△ABD为正三角形， Q为AD中点， ∴AD⊥BQ

∵PA=PD，Q为AD的中点，AD⊥PQ

又BQ∩PQ=Q  ∴AD⊥平面PQB， AD平面PAD

∴平面PQB⊥平面PAD

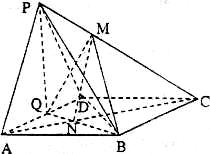（2）当时，平面

下面证明，若平面，连交于

由可得，，

平面，平面，平面平面，

   即：  

（3）由PA=PD=AD=2， Q为AD的中点，则PQ⊥AD。

    又平面PAD⊥平面ABCD，所以PQ⊥平面ABCD，

    以Q为坐标原点，分别以QA、QB、QP所在的直线为轴，建立如图所示的坐标系，则各点坐标为A（1，0，0），B（），Q（0，0，0），P（0，0，）

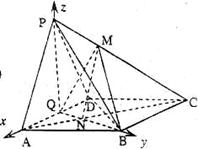    设平面MQB的法向量为，可得

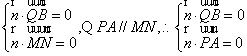    ，解得

    取平面ABCD的法向量

    故二面角的大小为60°