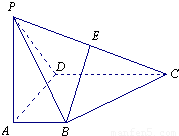
题目内容
如图,四棱锥P-ABCD的底面ABCD为直角梯形,PA⊥底面ABCD其中AB⊥AD,CD⊥AD,CD=AD=PA=2AB,E是PC中点.(1)求证:BE∥平面PAD;
(2)求异面直线PD与BC所成角的余弦值.
【答案】分析:(1)利用三角形的中位线定理和线面平行的判定定理即可证明;
(2)先作出异面直线所成的角,再使用余弦定理即可求出.
解答:解:(1)取PD中点F,连接EF,AF,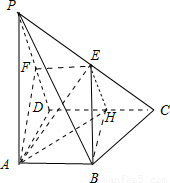
∵E是PC的中点,∴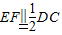 ,
,
又∵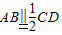 ,∴
,∴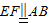 ,
,
∴四边形ABEF是平行四边形,∴BE∥AF,
∵BE?平面PAD,AF?平面PAD,
∴BE∥平面PAD.
(2)取CD的中点H,连接AH、EH、AE、BH,
∵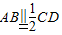 ,∴
,∴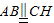 ,
,
∴四边形ABCH为平行四边形,∴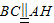 .
.
令AB=1,
在Rt△ADH中,由勾股定理得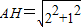 =
=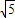 .
.
∵PA⊥底面ABCD,∴PA⊥AD,
∴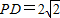 ,AF=
,AF=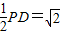 .
.
∵四边形ABHD为平行四边形,AD⊥AB,
∴四边形ABHD为矩形,∴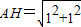 =
=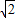 .
.
由三角形的中位线定理可知: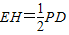 =
=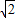 ,
,
由以上作法可知:∠AHE或其补角即为异面直线PD与BC所成的角.
∵PA⊥AB,AB⊥AD,
∴AB⊥平面PAD,∴AB⊥AF.
又∵四边形ABEF是平行四边形,∴四边形ABEF为矩形,
∴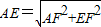 =
=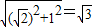 .
.
在△AEH中,由余弦定理得cos∠AHE=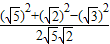 =
=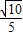 .
.
因此异面直线PD与BC所成角的余弦值为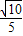 .
.
点评:熟练掌握线面平行与垂直的判定定理和性质定理及异面直线所成的角是解题的关键.注意使用三角形的中位线定理和平行四边形的判定定理及性质定理.
(2)先作出异面直线所成的角,再使用余弦定理即可求出.
解答:解:(1)取PD中点F,连接EF,AF,

∵E是PC的中点,∴
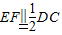 ,
,又∵
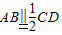 ,∴
,∴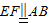 ,
,∴四边形ABEF是平行四边形,∴BE∥AF,
∵BE?平面PAD,AF?平面PAD,
∴BE∥平面PAD.
(2)取CD的中点H,连接AH、EH、AE、BH,
∵
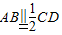 ,∴
,∴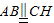 ,
,∴四边形ABCH为平行四边形,∴
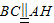 .
.令AB=1,
在Rt△ADH中,由勾股定理得
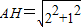 =
=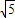 .
.∵PA⊥底面ABCD,∴PA⊥AD,
∴
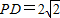 ,AF=
,AF=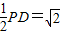 .
.∵四边形ABHD为平行四边形,AD⊥AB,
∴四边形ABHD为矩形,∴
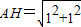 =
=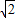 .
.由三角形的中位线定理可知:
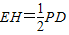 =
=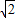 ,
,由以上作法可知:∠AHE或其补角即为异面直线PD与BC所成的角.
∵PA⊥AB,AB⊥AD,
∴AB⊥平面PAD,∴AB⊥AF.
又∵四边形ABEF是平行四边形,∴四边形ABEF为矩形,
∴
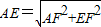 =
=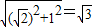 .
.在△AEH中,由余弦定理得cos∠AHE=
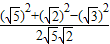 =
=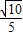 .
.因此异面直线PD与BC所成角的余弦值为
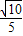 .
.点评:熟练掌握线面平行与垂直的判定定理和性质定理及异面直线所成的角是解题的关键.注意使用三角形的中位线定理和平行四边形的判定定理及性质定理.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=