题目内容
已知函数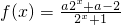 是奇函数.
是奇函数.
(1)求a值和函数f(x)的反函数f-1(x);
(2)若当x∈(-1,1)时,不等式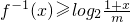 恒成立,求m取值范围.
恒成立,求m取值范围.
解:(1)∵f(x)是奇函数,∴ ,∴a=1…(2分)
,∴a=1…(2分)
记 .整理得
.整理得 ∴
∴
上式两边取2为底的对数,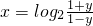 ,交换x、y,
,交换x、y,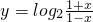
故所求反函数 …(8分)
…(8分)
(2)由(1)得 对x∈(-1,1)恒成立
对x∈(-1,1)恒成立
∵y=log2x是(0,+∞)上是增函数,
∴ …(11分)
…(11分)
即m≥1-x对x∈(-1,1)恒成立
故m的取值范围是m≥2…(13分)
分析:(1)根据f(x)是奇函数,则f(0)=0,可求出a的值,从而求出f(x)的解析式,根据指数的有界性求出函数的值域,将x用y表示,最后交换x、y,即可求出反函数的解析式,根据反函数的定义域即为原函数的值域可得所求;
(2)由(1)得 对x∈(-1,1)恒成立根据函数在(0,+∞)上的单调性建立不等式,将m分离出来,即m≥1-x对x∈(-1,1)恒成立,从而求出所求.
对x∈(-1,1)恒成立根据函数在(0,+∞)上的单调性建立不等式,将m分离出来,即m≥1-x对x∈(-1,1)恒成立,从而求出所求.
点评:本题主要考查了反函数,以及反函数与原函数的之间的关系,同时考查了恒成立问题和最值问题,是一道综合题.
 ,∴a=1…(2分)
,∴a=1…(2分)记
 .整理得
.整理得 ∴
∴
上式两边取2为底的对数,
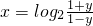 ,交换x、y,
,交换x、y,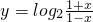
故所求反函数
 …(8分)
…(8分)(2)由(1)得
 对x∈(-1,1)恒成立
对x∈(-1,1)恒成立∵y=log2x是(0,+∞)上是增函数,
∴
 …(11分)
…(11分)即m≥1-x对x∈(-1,1)恒成立
故m的取值范围是m≥2…(13分)
分析:(1)根据f(x)是奇函数,则f(0)=0,可求出a的值,从而求出f(x)的解析式,根据指数的有界性求出函数的值域,将x用y表示,最后交换x、y,即可求出反函数的解析式,根据反函数的定义域即为原函数的值域可得所求;
(2)由(1)得
 对x∈(-1,1)恒成立根据函数在(0,+∞)上的单调性建立不等式,将m分离出来,即m≥1-x对x∈(-1,1)恒成立,从而求出所求.
对x∈(-1,1)恒成立根据函数在(0,+∞)上的单调性建立不等式,将m分离出来,即m≥1-x对x∈(-1,1)恒成立,从而求出所求.点评:本题主要考查了反函数,以及反函数与原函数的之间的关系,同时考查了恒成立问题和最值问题,是一道综合题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
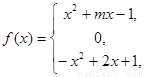
 是奇函数.
是奇函数.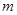 的值;
的值; 在区间
在区间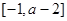 上单调递增,求实数
上单调递增,求实数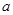 的取值范围;
的取值范围;
 是奇函数.
是奇函数.