Question

（09年莒南一中阶段性测评文）（12分）

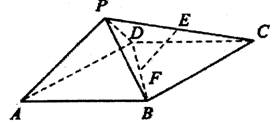
     如图，四棱锥P―ABCD中，ABCD为短形，△PAD为等腰直角三角形，∠APD=90°，面PAD⊥面ABCD，且AB=1，AD=2，E、F分别为PC和BD的中点。

   （I）证明：EF//面PAD；

   （II）证明：面PDC⊥面PAD；

   （III）求四棱锥P―ABCD的体积。

 

 

 

 

 

 

 

 

 

Answer 1

解析：（I）如图，连结AC，

   

 

 

 

 

 

 

 

∵ABCD为矩形，且F是BD的中点，

∴对角线AC必经过F   …………1分

又E是PC的中点，

∴EF∥AP   …………2分

∵EF在面PAD外，PA在面内，

∴EF∥PAD   …………4分

   （II）∵面PAD⊥面ABCD，CD⊥AD，面PAD∩面ABCD=AD，∴CD⊥面PAD，

又AP面PAD，∴AP⊥CD   …………6分

又∵AP⊥PD，PD和CD是相交直线，AP⊥面PCD   …………7分

又AD面PAD，所以面PDC⊥面PAD  …………8分

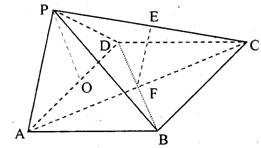
   （III）取AD中点为O，连结PO，

∵面PAD⊥面ABCD及△PAD为等腰直角三角形，

∴PO⊥面ABCD，

即PO为四棱锥P―ABCD的高  …………10分

∵AD=2，∴PO=1，

∴四棱锥P―ABCD的体积  …………12分