题目内容
已知抛物线的顶点为椭圆
+
=1（a＞b＞0）的中心．两曲线的焦点在同一坐标轴上，椭圆的长轴长为4．抛物线与椭圆交于点M(
，-
)，求抛物线方程与椭圆方程．
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
2
| ||
| 3 |
分析：由题意可设抛物线的方程为y2=mx（m≠0）．把点代入M(
，-
)抛物线方程即可得到m．把点M(
，-
)代入椭圆的方程可得
+
=1，又2a=4，联立即可解得．
| 2 |
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| 4 |
| 9a2 |
| 24 |
| 9b2 |
解答：解：∵椭圆的焦点在x轴上，且两曲线的焦点在同一坐标轴上，
∴抛物线的焦点也在x轴上，可设抛物线的方程为y2=mx（m≠0）．
∵M(
，-
)在抛物线上，∴(-
)2=
m，解得m=4，∴抛物线的方程为y2=4x．
∵M(
，-
)在椭圆上，∴
+
=1 ①
又2a=4 ②
由①②可得a2=4，b2=3．
∴椭圆的方程是
+
=1．
∴抛物线的焦点也在x轴上，可设抛物线的方程为y2=mx（m≠0）．
∵M(
| 2 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
∵M(
| 2 |
| 3 |
2
| ||
| 3 |
| 4 |
| 9a2 |
| 24 |
| 9b2 |
又2a=4 ②
由①②可得a2=4，b2=3．
∴椭圆的方程是
| x2 |
| 4 |
| y2 |
| 3 |
点评：本题考查了抛物线与椭圆的焦点的标准方程及其性质，属于基础题．
练习册系列答案
相关题目
的长轴长是焦距的两倍，其左、右焦点依次为
、
，抛物线
的准线与
轴交于
的一个交点为
.
时，求椭圆
过焦点
两点，若弦长
等于
的周长，求直线
和椭圆弧
）合成的曲线叫“抛椭圆”,是否存在以原点
为直角顶点，另两个顶点
落在“抛椭圆”上的等腰直角三角形
，若存在，求出两直角边所在直线的斜率；若不存在，说明理由.
的长轴长是焦距的两倍，其左、右焦点依次为
、
，抛物线
的准线与
轴交于
的一个交点为
.
时，求椭圆
过焦点
两点，若弦长
等于
的周长，求直线
和椭圆弧
）合成的曲线叫“抛椭圆”,是否存在以原点
为直角顶点，另两个顶点
落在“抛椭圆”上的等腰直角三角形
，若存在，求出两直角边所在直线的斜率；若不存在，说明理由.
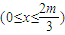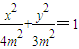
和椭圆弧
和椭圆弧
