题目内容
 如图,四棱柱ABCD-A1B1C1D1中,平面ACB1与底面ABCD垂直,B1A、B1B、B1C与底面ABCD的夹角均为45°,AD∥BC,且AB=BC=2,AD=1
如图,四棱柱ABCD-A1B1C1D1中,平面ACB1与底面ABCD垂直,B1A、B1B、B1C与底面ABCD的夹角均为45°,AD∥BC,且AB=BC=2,AD=1(1)求异面直线BB1与CD所成角的余弦值;
(2)求直线AC与平面AB1B所成角的余弦值;
(3)求三棱锥D1-ACB1的体积.
分析:(1)先根据条件作B1E⊥底面ABCD,得到E是AC的中点;建立如图所示的空间直角坐标系,得到各对应点的坐标,进而求出两直线所在向量的坐标,再代入向量的夹角计算公式即可.
(2)先求出平面的法向量,再根据利用向量求线面角的方法一步步进行即可;
(3)先根据条件求出D1到平面ACB1的距离,再代入体积计算公式即可.
(2)先求出平面的法向量,再根据利用向量求线面角的方法一步步进行即可;
(3)先根据条件求出D1到平面ACB1的距离,再代入体积计算公式即可.
解答:解(1):因为四棱柱ABCD-A1B1C1D1中,平面ACB1与底面ABCD垂直,B1A、B1B、B1C与底面ABCD的夹角均为45°,AD∥BC,且AB=BC=2,AD=1;
所以:作B1E⊥底面ABCD,此时E是AC的中点;
AE=BE=CE;∴∠ABC=90°.
∴△ABC为等腰直角三角形.AC=2
,CE=AE=
=B1E.
∵AD∥BC;
∴底面ABCD为直角梯形.

过点E分别作AD,AB的平行线,并分别以其为X轴,Y轴,以B1E所在的直线为Z轴.
则在下底面内B(1,-1,0),C(1,1,0),E(0,0,0),A(-1,-1,0),D(-1,0,0);B1(0,0,
).D1(-2,1,
).
∴
=(-1,1,
),
=(-2,-1,0);
=(-2,-2,0),
=(2,0,0).
∴cos<
,
>=
=
=
.
(2)设平面AB1B的一个法向量
=(x,y,z)
因为
=(2,0,0),
=(1,1,
).
则
⇒
⇒
=(0,-
,1).
∴cos<
,
>=cosθ=
=
=-
.
∴直线AC与平面AB1B所成角的余弦值cos(
-θ)=sinθ=
=
.
(3)由第一问得
=(1,-2,-
).
设平面ACB1的一个法向量
=(a,b,c)
则
⇒
⇒
=(1,-1,0)
∴D1到平面ACB1的距离d=
=
=
.
又S△ACB1=
AB1•B1C=
×2×2=2.
故三棱锥D1-ACB1的体积v=
S△ACB1.d=
×2×
=
.
所以:作B1E⊥底面ABCD,此时E是AC的中点;
AE=BE=CE;∴∠ABC=90°.
∴△ABC为等腰直角三角形.AC=2
| 2 |
| 2 |
∵AD∥BC;
∴底面ABCD为直角梯形.

过点E分别作AD,AB的平行线,并分别以其为X轴,Y轴,以B1E所在的直线为Z轴.
则在下底面内B(1,-1,0),C(1,1,0),E(0,0,0),A(-1,-1,0),D(-1,0,0);B1(0,0,
| 2 |
| 2 |
∴
| BB 1 |
| 2 |
| CD |
| AC |
| AB |
∴cos<
| BB 1 |
| CD |
| ||||
|
|
| 2-1 | ||
2×
|
| ||
| 10 |
(2)设平面AB1B的一个法向量
| n |
因为
| AB |
| AB1 |
| 2 |
则
|
|
| n |
| 2 |
∴cos<
| AC |
| n |
| ||||
|
|
-2
| ||||
2
|
| ||
| 3 |
∴直线AC与平面AB1B所成角的余弦值cos(
| π |
| 2 |
| 1-cos 2θ |
| ||
| 3 |
(3)由第一问得
| D 1A |
| 2 |
设平面ACB1的一个法向量
| e |
则
|
|
| e |
∴D1到平面ACB1的距离d=
|cos<
| ||||
|
|
| 1+2 | ||
|
3
| ||
| 2 |
又S△ACB1=
| 1 |
| 2 |
| 1 |
| 2 |
故三棱锥D1-ACB1的体积v=
| 1 |
| 3 |
| 1 |
| 3 |
3
| ||
| 2 |
| 2 |
点评:本题是道难题.它的难点在于不是直棱柱,空间直角坐标系的建立比较麻烦,本题适合程度较高的学生来做.

练习册系列答案
相关题目
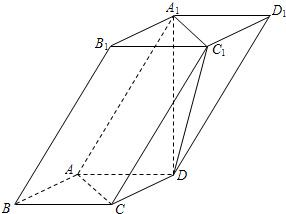 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.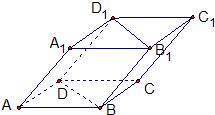 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是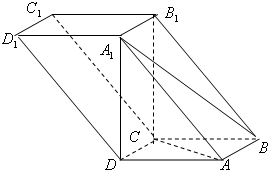 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2, (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD. (2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
(2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,