题目内容
已知点 ,直线
,直线 ,动点
,动点 到点
到点 的距离等于它到直线
的距离等于它到直线 的距离.
的距离.
(Ⅰ)试判断点 的轨迹
的轨迹 的形状,并写出其方程.
的形状,并写出其方程.
(Ⅱ)是否存在过 的直线
的直线 ,使得直线
,使得直线 被截得的弦
被截得的弦 恰好被点
恰好被点 所平分?
所平分?
本小题考查抛物线的标准方程、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想等.满分13分.
解:(Ⅰ)因点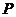 到点
到点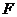 的距离等于它到直线
的距离等于它到直线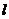 的距离,所以点
的距离,所以点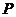 的轨迹
的轨迹 是以
是以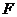 为焦点、直线
为焦点、直线 为准线的抛物线, ………………2分
为准线的抛物线, ………………2分
其方程为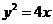 .
………………5分
.
………………5分
(Ⅱ)解法一:假设存在满足题设的直线 .设直线
.设直线 与轨迹
与轨迹 交于
交于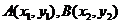 ,
,
依题意,得 .
………………6分
.
………………6分
①当直线 的斜率不存在时,不合题意. ………………7分
的斜率不存在时,不合题意. ………………7分
②当直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为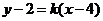 ,………8分
,………8分
联立方程组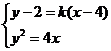 ,
,
消去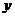 ,得
,得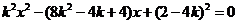 ,(*) ………………9分
,(*) ………………9分
∴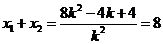 ,解得
,解得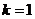 .
………………10分
.
………………10分
此时,方程(*)为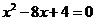 ,其判别式大于零, ………………11分
,其判别式大于零, ………………11分
∴存在满足题设的直线 ………………12分
………………12分
且直线 的方程为:
的方程为: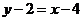 即
即 .
………………13分
.
………………13分
解法二:假设存在满足题设的直线 .设直线
.设直线 与轨迹
与轨迹 交于
交于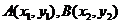 ,
,
依题意,得 .
………………6分
.
………………6分
易判断直线 不可能垂直
不可能垂直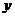 轴, ………………7分
轴, ………………7分
∴设直线 的方程为
的方程为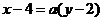 ,………8分
,………8分
联立方程组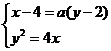 ,
,
消去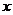 ,得
,得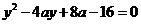 , ………………9分
, ………………9分
∵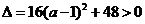 ,
,
∴直线与轨迹 必相交. ………………10分
必相交. ………………10分
又 ,∴
,∴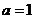 .
………………11分
.
………………11分
∴存在满足题设的直线 ………………12分
………………12分
且直线 的方程为:
的方程为: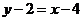 即
即 .
………………13分
.
………………13分
解法三:假设存在满足题设的直线 .设直线
.设直线 与轨迹
与轨迹 交于
交于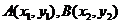 ,
,
依题意,得 .
………………6分
.
………………6分
∵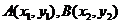 在轨迹
在轨迹 上,
上,
∴有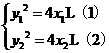 ,将
,将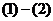 ,得
,得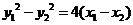 .
………8分
.
………8分
当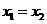 时,弦
时,弦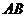 的中点不是
的中点不是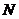 ,不合题意, ………9分
,不合题意, ………9分
∴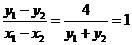 ,即直线
,即直线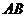 的斜率
的斜率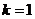 ,
………10分
,
………10分
注意到点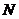 在曲线
在曲线 的张口内(或:经检验,直线
的张口内(或:经检验,直线 与轨迹
与轨迹 相交)…11分
相交)…11分
∴存在满足题设的直线 ………………12分
………………12分
且直线 的方程为:
的方程为: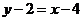 即
即 .
………………13分
.
………………13分
