题目内容
椭圆 与双曲线
与双曲线 有公共的焦点F1,F2,P是两曲线的一个交点,则cos∠F1PF2=( )
有公共的焦点F1,F2,P是两曲线的一个交点,则cos∠F1PF2=( )A.

B.

C.

D.

【答案】分析:利用双曲线、椭圆的定义,建立方程,求出|PF1|= ,|PF2|=
,|PF2|= ,再利用余弦定理,即可求得结论.
,再利用余弦定理,即可求得结论.
解答:解:不妨令P在双曲线的右支上,由双曲线的定义|PF1|-|PF2|=2 ①
①
由椭圆的定义|PF1|+|PF2|=2 ②
②
由①②可得|PF1|= ,|PF2|=
,|PF2|=
∵|F1F2|=4
∴cos∠F1PF2= =
=
故选A.
点评:本题考查圆锥曲线的共同特征,利用双曲线、椭圆的定义,建立方程是关键.
 ,|PF2|=
,|PF2|= ,再利用余弦定理,即可求得结论.
,再利用余弦定理,即可求得结论.解答:解:不妨令P在双曲线的右支上,由双曲线的定义|PF1|-|PF2|=2
 ①
①由椭圆的定义|PF1|+|PF2|=2
 ②
②由①②可得|PF1|=
 ,|PF2|=
,|PF2|=
∵|F1F2|=4
∴cos∠F1PF2=
 =
=
故选A.
点评:本题考查圆锥曲线的共同特征,利用双曲线、椭圆的定义,建立方程是关键.

练习册系列答案
相关题目




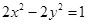 有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是 .
有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是 .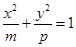 与双曲线
与双曲线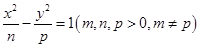 有公共的焦点
有公共的焦点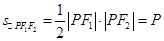
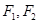 ,其交点为
,其交点为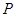 且∠
且∠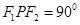 ,则△
,则△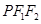 的面积是( )
的面积是( )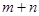 B.
B. 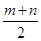 C.
C. 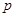 D.
D. 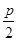
 与双曲线
与双曲线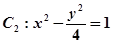 有公共的焦点,
有公共的焦点, 的一条渐近线与以
的一条渐近线与以 的长轴为直径的圆相交于A,B两点,若
的长轴为直径的圆相交于A,B两点,若 =
=