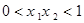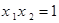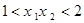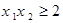题目内容
(本小题满分13分)已知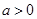 且
且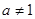 ,
,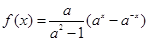
(1)判断函数 的奇偶性;
的奇偶性;
(2) 判断函数 的单调性,并证明;
的单调性,并证明;
(3)当函数 的定义域为
的定义域为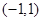 时,求使
时,求使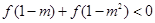 成立的实数
成立的实数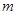 的取值范围.
的取值范围.
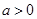 且
且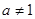 ,
,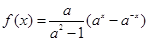
(1)判断函数
 的奇偶性;
的奇偶性;(2) 判断函数
 的单调性,并证明;
的单调性,并证明;(3)当函数
 的定义域为
的定义域为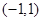 时,求使
时,求使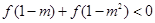 成立的实数
成立的实数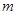 的取值范围.
的取值范围. (1) 为奇函数;(2)当
为奇函数;(2)当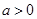 且
且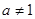 时,
时, 在
在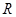 上是增函数;(3)
上是增函数;(3)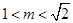 。
。
 为奇函数;(2)当
为奇函数;(2)当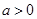 且
且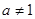 时,
时, 在
在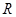 上是增函数;(3)
上是增函数;(3)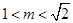 。
。本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.
(I)先求得f(x),令x=y=0,有f(0)=0,再令x1=x,x2=-x,即f(-x)=-f(x),故f(x)为奇函数.
(II)在R上任取x1<x2,则x1-x2<0,再比较f(x1)和f(x2)的大小,从而得出:f(x)是增函数;
(III)由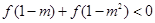 得
得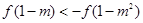 ,结合上一问单调性得到求解。
,结合上一问单调性得到求解。
解:(1)函数 的定义域是
的定义域是 ,关于原点对称
,关于原点对称
又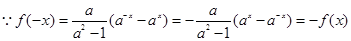 ,
,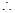
 为奇函数……………4分
为奇函数……………4分
(2)函数 在
在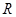 上为增函数
上为增函数
设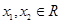 ,且
,且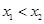 ,
,
则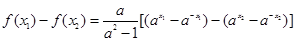
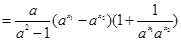
当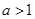 时,
时,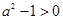 ,
,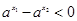 ,
,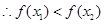
当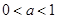 时,
时,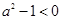 ,
,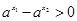 ,
,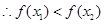
 当
当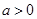 且
且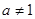 时,
时, 在
在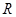 上是增函数……………9分
上是增函数……………9分
解法2: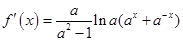 ,当
,当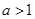 时,
时,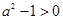 ,
,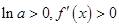 ,当
,当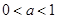 时,
时,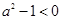 ,
,
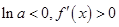
 当
当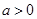 且
且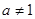 时,
时, 在
在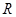 上是增函数……………9分
上是增函数……………9分
(3)由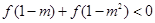 得
得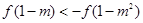 ,
,
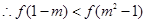 ,……………10分
,……………10分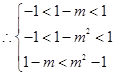 ……………11分
……………11分
解得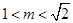 ……………13分
……………13分
(I)先求得f(x),令x=y=0,有f(0)=0,再令x1=x,x2=-x,即f(-x)=-f(x),故f(x)为奇函数.
(II)在R上任取x1<x2,则x1-x2<0,再比较f(x1)和f(x2)的大小,从而得出:f(x)是增函数;
(III)由
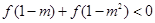 得
得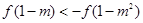 ,结合上一问单调性得到求解。
,结合上一问单调性得到求解。解:(1)函数
 的定义域是
的定义域是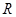 ,关于原点对称
,关于原点对称又
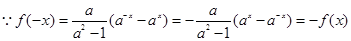 ,
,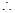
 为奇函数……………4分
为奇函数……………4分(2)函数
 在
在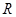 上为增函数
上为增函数设
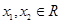 ,且
,且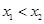 ,
,则
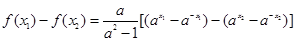
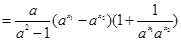
当
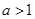 时,
时,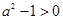 ,
,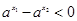 ,
,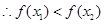
当
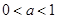 时,
时,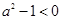 ,
,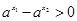 ,
,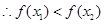
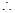 当
当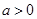 且
且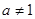 时,
时, 在
在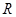 上是增函数……………9分
上是增函数……………9分解法2:
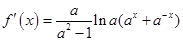 ,当
,当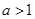 时,
时,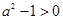 ,
,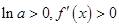 ,当
,当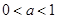 时,
时,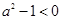 ,
,
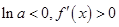
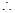 当
当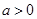 且
且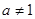 时,
时, 在
在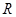 上是增函数……………9分
上是增函数……………9分(3)由
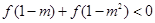 得
得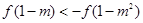 ,
,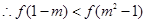 ,……………10分
,……………10分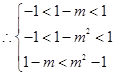 ……………11分
……………11分解得
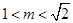 ……………13分
……………13分
练习册系列答案
相关题目
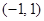 上的函数
上的函数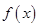 满足:
满足: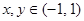 ,都有
,都有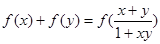
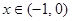 时,有
时,有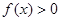 ,求证:(Ⅰ)
,求证:(Ⅰ)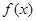 是奇函数;
是奇函数;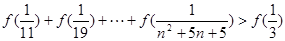
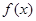 在区间
在区间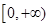 单调增加,则满足
单调增加,则满足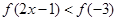 的
的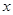 取值范围是
取值范围是 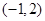
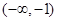
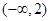
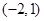
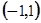 的函数
的函数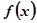
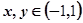 都有
都有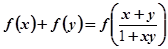 ;
;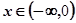 时,
时,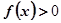 ,回答下列问题:
,回答下列问题: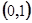 的单调性,并说明理由;
的单调性,并说明理由;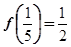 ,求
,求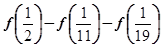 的值.
的值. 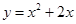 在闭区间
在闭区间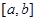 上的值域为
上的值域为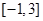 ,则满足题意的有序实数对
,则满足题意的有序实数对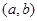 在坐标平面内所对应点组成图形的长度为 .
在坐标平面内所对应点组成图形的长度为 .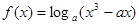
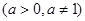 在区间
在区间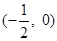 内单调递增,则
内单调递增,则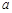 的取值范围是( )
的取值范围是( )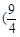 ,
,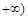
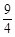 )
)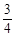 ,1)
,1)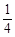 ,1)
,1)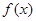 的定义域为D,若对于任意
的定义域为D,若对于任意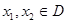 ,当
,当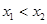 时,都有
时,都有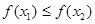 ,则称函数
,则称函数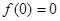 ;②
;② 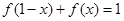
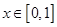 ; ③ 当
; ③ 当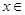
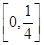 时,
时,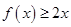 恒成立.则
恒成立.则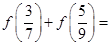 .
.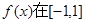 上是单调函数,且
上是单调函数,且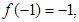 若函数
若函数 对所有的
对所有的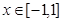 都成立,当
都成立,当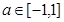 时,则
时,则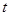 的取值范围是
的取值范围是 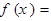
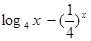 、
、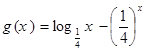 的零点分别为
的零点分别为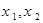 ,则( )
,则( )