题目内容
已知函数![]() 在区间
在区间![]() 上是增函数,
上是增函数,![]() 在区间
在区间![]() 上为减函数.
上为减函数.
(1)求实数![]() 的值;
的值;
(2)设函数![]() 是区间
是区间![]() 上的增函数,且对于
上的增函数,且对于![]() 内的任意两个变量
内的任意两个变量![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,求证:
,求证:![]() .
.
解:(1) ∵![]() ,依题意
,依题意![]() ,
,
∴![]() ,∴
,∴![]()
又∵![]() ,依题意
,依题意![]()
∴![]() ,∴
,∴![]()
∴![]()
(2)由(1)可知![]()
∴![]() 在
在![]() 上为减函数,且
上为减函数,且![]()
∵![]() 在
在![]() 上为增函数,∴
上为增函数,∴![]()
∴![]() ,∴
,∴![]()
又∵在![]() 上
上![]() ,∴依题意有
,∴依题意有![]()
∴![]()
(3)证明:∵![]()
①当![]() 时,
时,![]() ,原式成立
,原式成立
②当![]() 时,
时,![]()
![]()
![]()
![]()
![]()
由已知![]() ,
,![]() ,∴原不等式成立
,∴原不等式成立
∴综上所述,![]()

练习册系列答案
相关题目
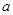 为常数,已知函数
为常数,已知函数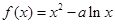 在区间
在区间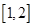 上是增函数,
上是增函数,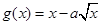 在区间
在区间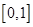 上是减函数.
上是减函数.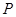 为函数
为函数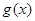 的图像上任意一点,求点
的图像上任意一点,求点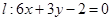 的距离的最小值;
的距离的最小值;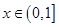 且
且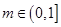 ,
,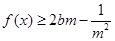 恒成立,求实数
恒成立,求实数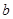 的取值范围.
的取值范围. 在区间
在区间 上是增函数,则实数
上是增函数,则实数 的取值范围是 .
的取值范围是 . 在区间
在区间 上是增函数,求
上是增函数,求 的取值范围
的取值范围 在区间
在区间 上是增函数,则实数
上是增函数,则实数 的取值范围是
的取值范围是  在区间
在区间 上是增函数,则
上是增函数,则 的取值范围是
( B )
的取值范围是
( B ) B.
B.
 D.
D.