题目内容
已知函数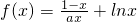 .
.
(Ⅰ)若函数f(x)在[1,+∞)上为增函数,求正实数a的取值范围;
(Ⅱ)当a=1时,求f(x)在 上的最大值和最小值.
上的最大值和最小值.
解:(Ⅰ)∵f(x)=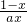 +lnx,
+lnx,
∴f'(x)=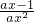 (a>0)
(a>0)
∵函数f(x)在[1,+∞)上为增函数
∴f'(x)=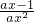 ≥0对 x∈[1,+∞)恒成立
≥0对 x∈[1,+∞)恒成立
∴ax-1≥0 在x∈[1,+∞)上恒成立
∴a≥ ,对x∈[1,+∞)恒成立
,对x∈[1,+∞)恒成立
∴a≥1.
(Ⅱ)当a=1时,f'(x)= .
.
当x∈[ ,1)时,f'(x)<0,故f(x)在x∈[
,1)时,f'(x)<0,故f(x)在x∈[ ,1)上单调递减;
,1)上单调递减;
当x∈[1,2]时,f'(x)>0,f(x)在x∈[1,2]上单调递增.
∴f(x)在x∈[ ,2]上有唯一极小值点,
,2]上有唯一极小值点,
故f(x)min=f(x)极小值=f(1)=0
∵f( )=1-ln2,f(2)=-
)=1-ln2,f(2)=- +ln2,f(
+ln2,f( )-f(2)=
)-f(2)= -2ln2=
-2ln2=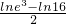 .
.
∵e3>16,∴f( )-f(2)>0?f(
)-f(2)>0?f( )>f(2).(10分)
)>f(2).(10分)
∴f(x)在区间[ ,2]上的最大值f(x)=f(
,2]上的最大值f(x)=f( )=1-ln2.
)=1-ln2.
综上可知,函数f(x)在 上的最大值是1-ln2,最小值是0.
上的最大值是1-ln2,最小值是0.
分析:(Ⅰ)先求出函数的导函数,把函数f(x)在[1,+∞)上为增函数转化为导函数大于等于0恒成立问题,再转化为关于正实数a的不等式问题即可求出正实数a的取值范围;
(Ⅱ)先求出函数的导函数以及导数为0的根,进而求出其在 上的单调性即可求f(x)在
上的单调性即可求f(x)在 上的最大值和最小值.
上的最大值和最小值.
点评:本题第二问考查了利用导数求闭区间上函数的最值,求函数在闭区间[a,b]上的最大值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到的.
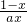 +lnx,
+lnx,∴f'(x)=
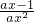 (a>0)
(a>0)∵函数f(x)在[1,+∞)上为增函数
∴f'(x)=
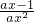 ≥0对 x∈[1,+∞)恒成立
≥0对 x∈[1,+∞)恒成立 ∴ax-1≥0 在x∈[1,+∞)上恒成立
∴a≥
 ,对x∈[1,+∞)恒成立
,对x∈[1,+∞)恒成立 ∴a≥1.
(Ⅱ)当a=1时,f'(x)=
 .
.当x∈[
 ,1)时,f'(x)<0,故f(x)在x∈[
,1)时,f'(x)<0,故f(x)在x∈[ ,1)上单调递减;
,1)上单调递减;当x∈[1,2]时,f'(x)>0,f(x)在x∈[1,2]上单调递增.
∴f(x)在x∈[
 ,2]上有唯一极小值点,
,2]上有唯一极小值点,故f(x)min=f(x)极小值=f(1)=0
∵f(
 )=1-ln2,f(2)=-
)=1-ln2,f(2)=- +ln2,f(
+ln2,f( )-f(2)=
)-f(2)= -2ln2=
-2ln2=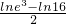 .
.∵e3>16,∴f(
 )-f(2)>0?f(
)-f(2)>0?f( )>f(2).(10分)
)>f(2).(10分)∴f(x)在区间[
 ,2]上的最大值f(x)=f(
,2]上的最大值f(x)=f( )=1-ln2.
)=1-ln2.综上可知,函数f(x)在
 上的最大值是1-ln2,最小值是0.
上的最大值是1-ln2,最小值是0.分析:(Ⅰ)先求出函数的导函数,把函数f(x)在[1,+∞)上为增函数转化为导函数大于等于0恒成立问题,再转化为关于正实数a的不等式问题即可求出正实数a的取值范围;
(Ⅱ)先求出函数的导函数以及导数为0的根,进而求出其在
 上的单调性即可求f(x)在
上的单调性即可求f(x)在 上的最大值和最小值.
上的最大值和最小值.点评:本题第二问考查了利用导数求闭区间上函数的最值,求函数在闭区间[a,b]上的最大值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到的.

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数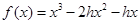 ,若
,若 且
且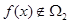 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得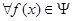 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
已知函数![]() 的定义域为
的定义域为![]() ,若
,若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“二阶比增函数”.
为“二阶比增函数”.
我们把所有“一阶比增函数”组成的集合记为![]() ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为![]() .
.
(Ⅰ)已知函数![]() ,若
,若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)已知![]() ,
,![]() 且
且![]() 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证:![]() ;
;
(Ⅲ)定义集合![]()
请问:是否存在常数![]() ,使得
,使得![]() ,
,![]() ,有
,有![]() 成立?若存在,求出
成立?若存在,求出![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
已知函数![]() 的定义域为
的定义域为![]() ,若
,若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“二阶比增函数”.
为“二阶比增函数”.
我们把所有“一阶比增函数”组成的集合记为![]() ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为![]() .
.
(Ⅰ)已知函数![]() ,若
,若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)已知![]() ,
,![]() 且
且![]() 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
求证:![]() ;
;
(Ⅲ)定义集合![]()
请问:是否存在常数![]() ,使得
,使得![]() ,
,![]() ,有
,有![]() 成立?若存在,求出
成立?若存在,求出![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


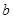
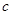




 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.