题目内容
已知偶函数f(x)(x∈R),当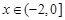 时,f(x)= -x(2+x),当
时,f(x)= -x(2+x),当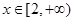 时,f(x)=(x-2)(a-x)(
时,f(x)=(x-2)(a-x)(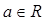 ).关于偶函数f(x)的图象G和直线
).关于偶函数f(x)的图象G和直线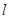 :y=m(
:y=m(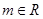 )的3个命题如下:
)的3个命题如下:
当a=2,m=0时,直线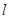 与图象G恰有3个公共点;
与图象G恰有3个公共点;
当a=3,m=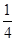 时,直线
时,直线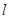 与图象G恰有6个公共点;
与图象G恰有6个公共点;
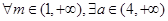 ,使得直线
,使得直线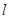 与图象G交于4个点,且相邻点之间的距离相等.其中正确命题的序号是(A)
与图象G交于4个点,且相邻点之间的距离相等.其中正确命题的序号是(A)
A. ①② B. ①③ C. ②③ D. ①②③
【答案】
A
【解析】
试题分析:根据题意,由于偶函数f(x)(x∈R),当 时,f(x)= -x(2+x),当
时,f(x)= -x(2+x),当 时,f(x)=(x-2)(a-x)(
时,f(x)=(x-2)(a-x)( ),那么可知函数当a=2,m=0时,则可知
),那么可知函数当a=2,m=0时,则可知 时,f(x)=(x-2)(2-x)=-(2-x)
时,f(x)=(x-2)(2-x)=-(2-x) ,那么可知偶函数关于y轴对称,则可知偶函数f(x)的图象G和直线
,那么可知偶函数关于y轴对称,则可知偶函数f(x)的图象G和直线 :y=0(
:y=0( )的交点为3个,故命题1成立,对于,当a=3,m=
)的交点为3个,故命题1成立,对于,当a=3,m= 时,直线
时,直线 与图象G恰有6个公共点;成立,对于
与图象G恰有6个公共点;成立,对于 ,使得直线
,使得直线 与图象G交于4个点,且相邻点之间的距离相等,错误故选A.
与图象G交于4个点,且相邻点之间的距离相等,错误故选A.
考点:函数的性质
点评:主要是考查了函数性质的运用,属于中档题。

练习册系列答案
相关题目
已知偶函数f(x+
),当x∈(-
,
)时,f(x)=x
+sinx,设a=f(1),b=f(2),c=f(3),则( )
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 3 |
| A、a<b<c |
| B、b<c<a |
| C、c<b<a |
| D、c<a<b |