题目内容
当x＞2时，使不等式x+
≥a恒成立的实数a的取值范围是______．
| 1 |
| x-2 |
∵x＞2
∴x-2＞0
∴x+
=（x-2）+
+2≥2
+2=4
而不等式x+
≥a恒成立
∴（x+
）min≥a
∴a的取值范围是（-∞，4]
故答案为（-∞，4]
∴x-2＞0
∴x+
| 1 |
| x-2 |
| 1 |
| x-2 |
(x-2)•
|
而不等式x+
| 1 |
| x-2 |
∴（x+
| 1 |
| x-2 |
∴a的取值范围是（-∞，4]
故答案为（-∞，4]
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
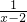≥a恒成立的实数a的取值范围是________．
≥a恒成立的实数a的取值范围是 ．