题目内容
已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),(Ⅰ)求抛物线的标准方程;
(Ⅱ)与圆x2+(y+1)2=1相切的直线l:y=kx+t交抛物线于不同的两点M,N,若抛物线上一点C满足
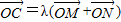 (λ>0),求λ的取值范围.
(λ>0),求λ的取值范围.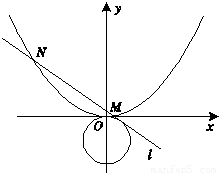
【答案】分析:(Ⅰ) 设抛物线方程为x2=2py,把点(2,1)代入求得p即可;
(II) 因为直线与圆相切,利用相切的性质即可得出k与t 的关系式,再把直线的方程与抛物线的方程联立得到关于x的一元二次方程,利用判别式△>0得到t的取值范围,利用根与系数的关系及已知满足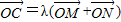 (λ>0),即可得出λ的取值范围.
(λ>0),即可得出λ的取值范围.
解答: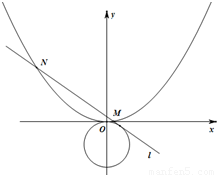 解(Ⅰ) 设抛物线方程为x2=2py,
解(Ⅰ) 设抛物线方程为x2=2py,
由已知得:22=2p所以 p=2
所以抛物线的标准方程为 x2=4y.
(Ⅱ) 因为直线与圆相切,
所以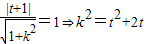
把直线方程代入抛物线方程并整理得:x2-4kx-4t=0
由△=16k2+16t=16(t2+2t)+16t>0
得 t>0或t<-3
设M(x1,y1),N(x2,y2),
则x1+x2=4k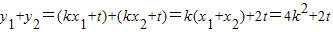
由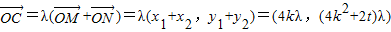
得 C(4kλ,(4k2+2t)λ)
因为点C在抛物线x2=4y上,
所以,16k2λ2=4(4k2+2t)λ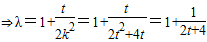
因为t>0或t<-3,
所以 2t+4>4或 2t+4<-2
所以 λ的取值范围为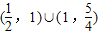 .
.
点评:本题主要考查抛物线的方程与性质、直线方程、直线与抛物线及圆的位置关系等基础知识,考查运算能力、推理论证以及分析问题、解决问题的能力.
(II) 因为直线与圆相切,利用相切的性质即可得出k与t 的关系式,再把直线的方程与抛物线的方程联立得到关于x的一元二次方程,利用判别式△>0得到t的取值范围,利用根与系数的关系及已知满足
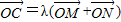 (λ>0),即可得出λ的取值范围.
(λ>0),即可得出λ的取值范围.解答:
 解(Ⅰ) 设抛物线方程为x2=2py,
解(Ⅰ) 设抛物线方程为x2=2py,由已知得:22=2p所以 p=2
所以抛物线的标准方程为 x2=4y.
(Ⅱ) 因为直线与圆相切,
所以
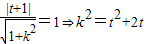
把直线方程代入抛物线方程并整理得:x2-4kx-4t=0
由△=16k2+16t=16(t2+2t)+16t>0
得 t>0或t<-3
设M(x1,y1),N(x2,y2),
则x1+x2=4k
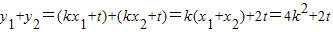
由
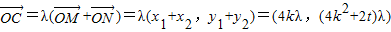
得 C(4kλ,(4k2+2t)λ)
因为点C在抛物线x2=4y上,
所以,16k2λ2=4(4k2+2t)λ
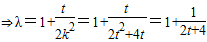
因为t>0或t<-3,
所以 2t+4>4或 2t+4<-2
所以 λ的取值范围为
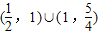 .
.点评:本题主要考查抛物线的方程与性质、直线方程、直线与抛物线及圆的位置关系等基础知识,考查运算能力、推理论证以及分析问题、解决问题的能力.

练习册系列答案
相关题目
 ,它们在
,它们在 轴上有共同焦点,抛物线的顶点为坐
轴上有共同焦点,抛物线的顶点为坐