题目内容
（本小题满分12分）
如图，直平行六面体ABCD－A1B1C1D1的高为3，
底面是边长为4， 且∠BAD＝60°的菱形，AC∩
BD＝O，A1C1∩B1D1＝O1，E是线段AO1上一点．
（Ⅰ）求点A到平面O1BC的距离；
（Ⅱ）当AE为何值时，二面角E－BC－D的大小为
.
【答案】
(1) 
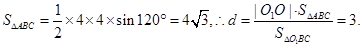
(2) AE=AO1=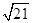
【解析】解：(Ⅰ) 设A到平面O1BC距离为d.
由
，得 
.
由直四棱柱ABCD—A1B1C1D1的高为3，底面是边长为4且∠BAD=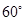
的菱形.
∴|O1B1|=
|A1B1|=2. ∴
.
∴
.
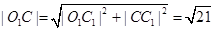由余弦定理得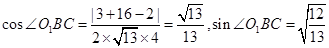
.
∴
.
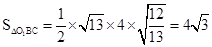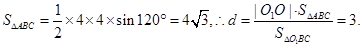…………………6分
(Ⅱ)过E作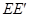
垂直AC，垂足为
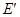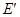，过作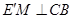
，垂足为M，连结EM .
由三垂线定理得EM⊥CB， ∴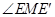
为二面角E—BC—D的平面角．
若
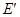，设M=x，则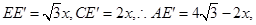
又
此时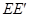与OO1重合，∴AE=AO1= 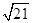．……………………………………12分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
