题目内容

若2∈{x|x（x-m）＜0，m∈Z}，则m的最小值为
3
3
．
分析：根据{x|x（x-m）＜0，m∈Z}对m进行分类讨论，m＞0，{x|x（x-m）＜0，m∈Z}={x|0＜x＜m，m∈Z}；m=0，根据x（x-m）＜0转化为x2＜0，而x2≥0，故舍去；m＜0，{x|x（x-m）＜0}={x|m＜x＜0，m∈Z}；在根据2∈{x|x（x-m）＜0，m∈Z}知{x|x（x-m）＜0，m∈Z}={x|0＜x＜m，m∈Z}即可求解
解答：解：当m＞0时
∴{x|x（x-m）＜0，m∈Z}={x|0＜x＜m，m∈Z}
  当m=0时
∴x（x-m）＜0转化为x2＜0，而x2≥0，故舍去
  m＜0时
∴{x|x（x-m）＜0}={x|m＜x＜0，m∈Z}
∵2∈{x|x（x-m）＜0，m∈Z}
∴{x|x（x-m）＜0，m∈Z}={x|0＜x＜m，m∈Z}
∴m的最小值为 3
故答案为3
点评：本题考查了集合关系中的参数取值问题，分类讨论也是解题的关键，属于基础题．
练习册系列答案
相关题目
对于定义在D上的函数y=f（x），若同时满足．
①存在闭区间[a，b]⊆D，使得任取x1∈[a，b]，都有f（x1）=c （c是常数）；
②对于D内任意x2，当x2∉[a，b]时总有f（x2）＞c称f（x）为“平底型”函数．
（1）（理）判断f1（x）=|x-1|+|x-2|，f2（x）=x+|x-2|是否是“平底型”函数？简要说明理由；
（文）判断f1（x）=|x-1|+|x-2|，f2（x）=x-|x-3|是否是“平底型”函数？简要说明理由；
（2）（理）设f（x）是（1）中的“平底型”函数，若|t-k|+|t+k|≥|k|•f（x），k∈R且k≠0，对一切t∈R恒成立，求实数x的范围；
（文）设f（x）是（1）中的“平底型”函数，若|t-1|+|t+1|≥f（x），对一切t∈R恒成立，求实数x的范围；
（3）（理）若F（x）=mx+
x2+2x+n
，x∈[-2，+∞）是“平底型”函数，求m和n的值；
（文）若F（x）=m|x-1|+n|x-2|是“平底型”函数，求m和n满足的条件．
已知函数f（x）是区间D⊆[0，+∞）上的增函数．若f（x）可表示为f（x）=f1（x）+f2（x），其中f1（x）是D上的增函数，f2（x）是D上的减函数，且函数f2（x）的值域A⊆[0，+∞），则称函数f（x）的区间D上的“偏增函数”
（1）试说明y=sinx+cosx是区间（0，
π
4
）上的“偏增函数”；
（2）记f1（x）=x，f2（x）=
a
x
（a为常数），是判断f（x）=f1（x）+f2（x）是否是区间（0，1]上的“偏增函数”，若是，证明你的结论，若不是，请说明理由．
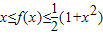设二次函数f（x）=ax2+bx+c（a≠0）满足条件：①当x∈R时，f（x-4）=f（2-x），且；②f（x）在R上的最小值为0．
（1）求f（1）的值及f（x）的解析式；
（2）若g（x）=f（x）-k2x在[-1，1]上是单调函数，求k的取值范围；
（3）求最大值m（m＞1），使得存在t∈R，只要x∈[1，m]，就有f（x+t）≤x．
下列说法：①若f(x)=ax2+（2a+b）x+2（其中x∈[2a-1，a+4]）是偶函数，则实数b=2；
②既是奇函数又是偶函数；
③已知f(x)是定义在R上的奇函数，若当x∈[0，+∞)时，f(x)=x(1+x)，则当x∈R时，f(x)=x(1+|x|)；
④已知f(x)是定义在R上的不恒为零的函数，且对任意的x，y∈R都满足f(x·y)=x·f(y)+y·f(x)，则f(x)是奇函数；
其中所有正确命题的序号是（    ）。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网