题目内容
自点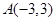 发出的光线
发出的光线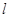 射到
射到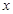 轴上,被
轴上,被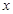 轴反射,其反射光线所在直线与圆
轴反射,其反射光线所在直线与圆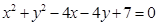 相切,求光线
相切,求光线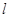 所在直线的方程。
所在直线的方程。
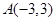 发出的光线
发出的光线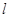 射到
射到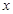 轴上,被
轴上,被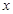 轴反射,其反射光线所在直线与圆
轴反射,其反射光线所在直线与圆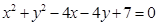 相切,求光线
相切,求光线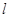 所在直线的方程。
所在直线的方程。 或
或 .
.试题分析:已知圆
 关于
关于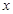 轴的对称圆
轴的对称圆 的方程为
的方程为 2分
2分如图所示.

可设光线
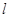 所在直线方程为
所在直线方程为 , 4分
, 4分∵直线
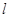 与圆
与圆 相切,
相切,∴圆心

 到直线
到直线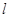 的距离
的距离 =
= , 6分
, 6分解得
 或
或 . 10分
. 10分∴光线
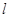 所在直线的方程为
所在直线的方程为 或
或 .…12分
.…12分点评:本题也可以这样做:求出点
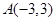 关于x轴的对称点
关于x轴的对称点 ,则反射光线一定过点
,则反射光线一定过点 ,由此设出直线方程,利用直线与圆相切求出即可。在设直线方程的点斜式时,要注意讨论直线的斜率是否存在。
,由此设出直线方程,利用直线与圆相切求出即可。在设直线方程的点斜式时,要注意讨论直线的斜率是否存在。
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 ,点
,点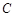 是圆
是圆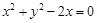 上任意一点,则
上任意一点,则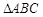 面积的最小值是( ).
面积的最小值是( ).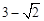
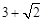
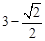
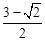
 与圆
与圆 相交于
相交于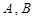 两点,且
两点,且 则
则 的值是
的值是 


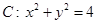 ,直线
,直线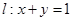 ,则圆C内任意一点到直线的距离小于
,则圆C内任意一点到直线的距离小于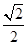 的概率为( )
的概率为( )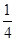
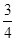
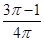
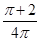
 恰有一个公共点,则b的取值范围为______
恰有一个公共点,则b的取值范围为______  上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )


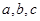 是直角三角形的三边(
是直角三角形的三边(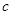 为斜边), 则圆
为斜边), 则圆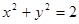 被直线
被直线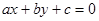 所截得的弦长等于__________.
所截得的弦长等于__________.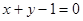 被圆
被圆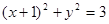 截得的弦长等于 。
截得的弦长等于 。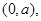 其斜率为1,且与圆
其斜率为1,且与圆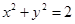 相切,则
相切,则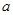 的值为
的值为