题目内容
【题目】已知命题![]() :直线
:直线![]() 与圆
与圆![]() 有两个交点;命题:
有两个交点;命题:![]() .
.
(1)若![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为真命题,
为真命题,![]() 为假命题,求实数
为假命题,求实数![]() 的取值范围.
的取值范围.
【答案】(1)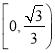 ;(2)
;(2) .
.
【解析】
试题分析:先求出![]() 分别为真命题时
分别为真命题时![]() 的取值范围:对命题
的取值范围:对命题![]() ,利用圆心到直线的距离小于半径,求得
,利用圆心到直线的距离小于半径,求得![]() .对命题
.对命题![]() ,利用三角恒等变形公式,将原不等式左边转化为
,利用三角恒等变形公式,将原不等式左边转化为![]() ,求得其值域为
,求得其值域为![]() ,故
,故![]() .(1)
.(1)![]() 且
且![]() 真,取
真,取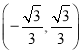 与
与![]() 的交集,得
的交集,得![]() ;(2)由于“
;(2)由于“![]() 为真命题,
为真命题,![]() 为假命题”所以分别求“
为假命题”所以分别求“![]() 真
真![]() 假”和“
假”和“![]() 假
假![]() 真”时
真”时![]() 的取值范围,然后取并集即可.
的取值范围,然后取并集即可.
试题解析:
∵![]() ,∴
,∴![]() ,
,
所以该圆的圆心为![]() ,半径为
,半径为![]() ,圆心到直线的距离
,圆心到直线的距离![]() .
.
若![]() 为真,则圆心到直线的距离小于半径,即
为真,则圆心到直线的距离小于半径,即![]() ,解得
,解得![]() .
.
若![]() 为真,则
为真,则![]() 在
在![]() 上有解,
上有解,
因为
![]() ,又由
,又由![]() ,得
,得![]() ,
,
所以![]() ,
,
即![]() ,故若
,故若![]() 为真,则
为真,则![]() ...................6分
...................6分
(1)若![]() 为真,则应满足
为真,则应满足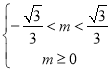 ,即
,即![]() ,
,
故实数![]() 的取值范围为
的取值范围为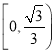 ....................8分
....................8分
(2)若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() 一真一假,
一真一假,
若![]() 真
真![]() 假,则应满足
假,则应满足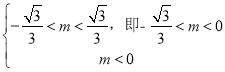 ,
,
若![]() 假
假![]() 真,则应满足
真,则应满足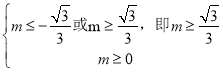
综上所述,实数![]() 的取值范围为
的取值范围为 ..............12分
..............12分

练习册系列答案
相关题目