题目内容
 (2010•南京三模)如图,正四棱锥P-ABCD中,AB=2,PA=
(2010•南京三模)如图,正四棱锥P-ABCD中,AB=2,PA=| 3 |
求:(1)直线BD与直线PC所成的角;
(2)平面PBC与平面PAC所成的角.
分析:(1)先根据条件得到OP⊥平面ABCD并求出OP=1;然后建立空间直角坐标系,求出各点坐标,进而求出
,
的坐标,通过计算其数量积即可得到结论.
(2)先求出两个平面的法向量,再代入向量的夹角计算公式即可得到答案.
| PC |
| BD |
(2)先求出两个平面的法向量,再代入向量的夹角计算公式即可得到答案.
解答: 解:(1)因为四棱锥P-ABCD为正四棱锥,
解:(1)因为四棱锥P-ABCD为正四棱锥,
0为AC,BD交点,所以OP⊥平面ABCD.
因为AB=2,所以OA=
,
因为PA=
.
所以OP2=PA2-OA2=3-2=1,
所以OP=1.
如图以O为原点,AC,BD所在直线分别为X轴,Y轴,建立空间直角坐标系.
则A(
,0,0),B(0,
,0),C(-
,0,0),D(0,-
,0),P(0,0,1),
则
=(-
,0,-1),
=(0,-2
,0).
因为
•
=0.
所以直线BD与直线PC所成的角:90°.
(2)由(1)得BD⊥PC,又BD⊥AC,PC?平面PAC,AC?平面PAC,PC∩AC=C,
所以BD⊥平面PAC,取平面PAC的一个法向量为
=(0,-2
,0).
设平面PBC的一个法向量为
=(x,y,z),
=(-
,-
,0).
由
得
,
不妨取
=(1,-1,-
),则cos<
,
>=
=
,
可得向量
与
的夹角为60°.
所以平面PBC与平面PAC所成的角为60°.
 解:(1)因为四棱锥P-ABCD为正四棱锥,
解:(1)因为四棱锥P-ABCD为正四棱锥,0为AC,BD交点,所以OP⊥平面ABCD.
因为AB=2,所以OA=
| 2 |
因为PA=
| 3 |
所以OP2=PA2-OA2=3-2=1,
所以OP=1.
如图以O为原点,AC,BD所在直线分别为X轴,Y轴,建立空间直角坐标系.
则A(
| 2 |
| 2 |
| 2 |
| 2 |
则
| PC |
| 2 |
| BD |
| 2 |
因为
| PC |
| BD |
所以直线BD与直线PC所成的角:90°.
(2)由(1)得BD⊥PC,又BD⊥AC,PC?平面PAC,AC?平面PAC,PC∩AC=C,
所以BD⊥平面PAC,取平面PAC的一个法向量为
| BD |
| 2 |
设平面PBC的一个法向量为
| n |
| BC |
| 2 |
| 2 |
由
|
|
不妨取
| n |
| 2 |
| n |
| BD |
| ||||
|
|
| 1 |
| 2 |
可得向量
| BD |
| n |
所以平面PBC与平面PAC所成的角为60°.
点评:本题主要考察用空间向量求平面间的夹角.用空间向量求平面间的夹角的关键问题在于两个平面的法向量不能求错.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
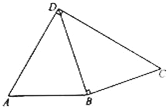 (2010•南京三模)如图,平面四边形ABCD中,∠A=60°,AD⊥CD,DB⊥BC,AB=2
(2010•南京三模)如图,平面四边形ABCD中,∠A=60°,AD⊥CD,DB⊥BC,AB=2