题目内容
正四面体ABCD外接球的体积为4
π,则点A到平面BCD的距离为:
.
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
分析:先确定球的半径,再把正四面体ABCD分成了4个全等的三棱锥,利用等体积,确定高的关系,即可得到结论.
解答:解:∵正四面体ABCD外接球的体积为4
π,∴球的半径是
设ABCD的中心是O,则OA=OB=OC=OD=R=
∵O把ABCD分成了4个全等的三棱锥
∴正四面体的体积=
×一个面的面积×四面体的高=4×
×一个面的面积×小三棱锥的高
∴ABCD的高(点A到平面BCD的距离)=4×小三棱锥的高(O到平面BCD的距离)
过A做平面BCD的垂线AH,则AH=4OH
∴点A到平面BCD的距离=AH=
AO=
故答案为:
| 3 |
| 3 |
设ABCD的中心是O,则OA=OB=OC=OD=R=
| 3 |
∵O把ABCD分成了4个全等的三棱锥
∴正四面体的体积=
| 1 |
| 3 |
| 1 |
| 3 |
∴ABCD的高(点A到平面BCD的距离)=4×小三棱锥的高(O到平面BCD的距离)
过A做平面BCD的垂线AH,则AH=4OH
∴点A到平面BCD的距离=AH=
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
故答案为:
| 4 |
| 3 |
| 3 |
点评:本题考查点面距离的计算,考查球的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
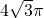 ,则点A到平面BCD的距离为:________.
,则点A到平面BCD的距离为:________. ,则点A到平面BCD的距离为: .
,则点A到平面BCD的距离为: .