题目内容
 (2012•乐山二模)如图,在棱长为2的正方体ABCD-A1B1C1D1中,M为棱BB1的中点.
(2012•乐山二模)如图,在棱长为2的正方体ABCD-A1B1C1D1中,M为棱BB1的中点.(1)求平面A1DM与平面ABCD所成的锐二面角的大小;
(2)求点B到平面A1DM的距离.
分析:(1)延长A1M,与AB的延长线交于点O,连接OD,过B作BE⊥DO,垂足为E,连接ME,则ME⊥DO,可得∠MEB为平面A1DM与平面ABCD所成的锐二面角的平面角;
(2)过点B做BF⊥ME,证明BF⊥平面A1DM,从而BF为点B到平面A1DM的距离,利用等面积,即可求BF⊥平面A1DM
∴BF为点B到平面A1DM的距离,
(2)过点B做BF⊥ME,证明BF⊥平面A1DM,从而BF为点B到平面A1DM的距离,利用等面积,即可求BF⊥平面A1DM
∴BF为点B到平面A1DM的距离,
解答: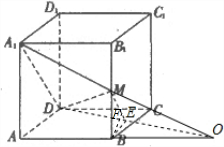 解:(1)延长A1M,与AB的延长线交于点O,连接OD,过B作BE⊥DO,垂足为E,连接ME,则ME⊥DO
解:(1)延长A1M,与AB的延长线交于点O,连接OD,过B作BE⊥DO,垂足为E,连接ME,则ME⊥DO
∴∠MEB为平面A1DM与平面ABCD所成的锐二面角的平面角
∵M为棱BB1的中点,棱长为2,
∴MB=1
∵DO•BE=AD•BO
∴BE=
∴tan∠MEB=
=
∴所求二面角的大小为arctan
;
(2)过点B做BF⊥ME,
由(1)知DO⊥平面MBE
∵DO?平面A1DM
∴平面A1DM⊥平面MBE
∵BF⊥ME,平面A1DM∩平面MBE=ME
∴BF⊥平面A1DM
∴BF为点B到平面A1DM的距离,
∵BE=
,MB=1
∴ME=
∵ME•BF=MB•BE
∴BF=
=
=
.
 解:(1)延长A1M,与AB的延长线交于点O,连接OD,过B作BE⊥DO,垂足为E,连接ME,则ME⊥DO
解:(1)延长A1M,与AB的延长线交于点O,连接OD,过B作BE⊥DO,垂足为E,连接ME,则ME⊥DO∴∠MEB为平面A1DM与平面ABCD所成的锐二面角的平面角
∵M为棱BB1的中点,棱长为2,
∴MB=1
∵DO•BE=AD•BO
∴BE=
2
| ||
| 5 |
∴tan∠MEB=
| MB |
| BE |
| ||
| 2 |
∴所求二面角的大小为arctan
| ||
| 2 |
(2)过点B做BF⊥ME,
由(1)知DO⊥平面MBE
∵DO?平面A1DM
∴平面A1DM⊥平面MBE
∵BF⊥ME,平面A1DM∩平面MBE=ME
∴BF⊥平面A1DM
∴BF为点B到平面A1DM的距离,
∵BE=
2
| ||
| 5 |
∴ME=
3
| ||
| 5 |
∵ME•BF=MB•BE
∴BF=
| MB•BE |
| ME |
1•
| ||||
|
| 2 |
| 3 |
点评:本题考查面面角,考查点到面的距离的计算,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•乐山二模)一个频率分布表(样本容量为30)不小心被损坏了一部分(如图),只记得样本中数据在[20,60)上的频率为0.8,则估计样本在[40,50),[50,60)内的数据个数可能是( )
(2012•乐山二模)一个频率分布表(样本容量为30)不小心被损坏了一部分(如图),只记得样本中数据在[20,60)上的频率为0.8,则估计样本在[40,50),[50,60)内的数据个数可能是( ) (2012•乐山二模)如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若AB=
(2012•乐山二模)如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若AB=