题目内容
若函数f(x)=4x2-kx-8在[5,8]上是单调函数,则k的取值范围是( )A.(-∞,40]
B.[40,64]
C.(-∞,40]∪[64,+∞)
D.[64,+∞)
【答案】分析:根据二次函数的性质知对称轴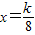 ,在[5,8]上是单调函数则对称轴不能在这个区间上,
,在[5,8]上是单调函数则对称轴不能在这个区间上,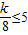 ,或
,或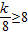 ,解出不等式组求出交集.
,解出不等式组求出交集.
解答:解:、根据二次函数的性质知对称轴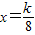 ,
,
在[5,8]上是单调函数则对称轴不能在这个区间上
∴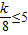 ,或
,或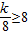 ,
,
得k≤40,或k≥64
故选C.
点评:本题考查二次函数的性质,本题解题的关键是看出二次函数在一个区间上单调,只有对称轴不在这个区间上,本题是一个基础题.
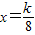 ,在[5,8]上是单调函数则对称轴不能在这个区间上,
,在[5,8]上是单调函数则对称轴不能在这个区间上,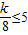 ,或
,或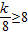 ,解出不等式组求出交集.
,解出不等式组求出交集.解答:解:、根据二次函数的性质知对称轴
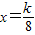 ,
,在[5,8]上是单调函数则对称轴不能在这个区间上
∴
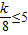 ,或
,或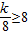 ,
,得k≤40,或k≥64
故选C.
点评:本题考查二次函数的性质,本题解题的关键是看出二次函数在一个区间上单调,只有对称轴不在这个区间上,本题是一个基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
若函数f(x)=
,则f(log43)=( )
|
A、
| ||
B、
| ||
| C、3 | ||
| D、4 |