题目内容
已知中心在原点,长轴在x轴上的椭圆的一个顶点是点(0,| 5 |
| ||
| 6 |
(1)求椭圆方程;
(2)点M在椭圆上,求△MF1F2面积的最大值;
(3)试探究椭圆上是否存在一点P,使
| PF1 |
| PF2 |
分析:(1)由题意设出椭圆标准方程,根据顶点的坐标和离心率得b=
,e=
=
,根据a2=b2+c2求出a的值,即求出椭圆标准方程;
(2)根据(1)求出的椭圆标准方程,求出点M纵坐标的范围,即求出三角形面积的最大值;
(3)先假设存在点P满足条件,根据向量的数量积得
⊥
,根据椭圆的焦距和椭圆的定义列出两个方程,求出S△PF1F2的值,结合(2)中三角形面积的最大值,判断出是否存在点P.
| 5 |
| c |
| a |
| ||
| 6 |
(2)根据(1)求出的椭圆标准方程,求出点M纵坐标的范围,即求出三角形面积的最大值;
(3)先假设存在点P满足条件,根据向量的数量积得
| PF1 |
| PF2 |
解答:解:(1)由题意设椭圆标准方程为
+
=1.
由已知得,b=
,e=
=
.(2分)
则e2=
=
=1-
,∴1-
=
.解得a2=6(4分)
∴所求椭圆方程为
+
=1(5分)
(2)令M(x1,y1),则S△MF1F2=
|F1F2|•|y1|=
•2•|y1|(7分)
∵点M在椭圆上,∴-
≤y1≤
,故|y1|的最大值为
(8分)
∴当y1=±
时,S△MF1F2的最大值为
.(9分)
(3)假设存在一点P,使
•
=0,
∵
≠
,
≠
,∴
⊥
,(10分)
∴△PF1F2为直角三角形,∴|PF1|2+|PF2|2=|F1F2|2=4 ①(11分)
又∵|PF1|+|PF2|=2a=2
②(12分)
∴②2-①,得2|PF1|•|PF2|=20,∴
|PF1|•|PF2|=5,(13分)
即S△PF1F2=5,由(1)得S△PF1F2最大值为
,故矛盾,
∴不存在一点P,使
•
=0.(14分)
| x2 |
| a2 |
| y2 |
| b2 |
由已知得,b=
| 5 |
| c |
| a |
| ||
| 6 |
则e2=
| c2 |
| a2 |
| a2-b2 |
| a2 |
| b2 |
| a2 |
| 5 |
| a2 |
| 1 |
| 6 |
∴所求椭圆方程为
| x2 |
| 6 |
| y2 |
| 5 |
(2)令M(x1,y1),则S△MF1F2=
| 1 |
| 2 |
| 1 |
| 2 |
∵点M在椭圆上,∴-
| 5 |
| 5 |
| 5 |
∴当y1=±
| 5 |
| 5 |
(3)假设存在一点P,使
| PF1 |
| PF2 |
∵
| PF1 |
| 0 |
| PF2 |
| 0 |
| PF1 |
| PF2 |
∴△PF1F2为直角三角形,∴|PF1|2+|PF2|2=|F1F2|2=4 ①(11分)
又∵|PF1|+|PF2|=2a=2
| 6 |
∴②2-①,得2|PF1|•|PF2|=20,∴
| 1 |
| 2 |
即S△PF1F2=5,由(1)得S△PF1F2最大值为
| 5 |
∴不存在一点P,使
| PF1 |
| PF2 |
点评:本题考查了椭圆方程的求法以及椭圆的性质、向量数量积的几何意义,利用a、b、c、e几何意义和a2=b2+c2求出a和b的值,根据椭圆上点的坐标范围求出相应三角形的面积最值,即根据此范围判断点P是否存在,此题综合性强,涉及的知识多,考查了分析问题和解决问题的能力.

练习册系列答案
相关题目
 ),离心率为
),离心率为 ,左、右焦点分别为F1和F2.
,左、右焦点分别为F1和F2.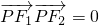 ,若存在,请求出点P的坐标;若不存在,请说明理由.
,若存在,请求出点P的坐标;若不存在,请说明理由. ),离心率为
),离心率为 ,左、右焦点分别为F1和F2.
,左、右焦点分别为F1和F2. ,若存在,请求出点P的坐标;若不存在,请说明理由.
,若存在,请求出点P的坐标;若不存在,请说明理由.