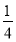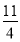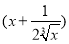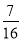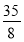题目内容
已知函数f(x)＝|2x－1|＋|2x＋a|，g(x)＝x＋3.
(1)当a＝－2时，求不等式f(x)<g(x)的解集；
(2)设a>－1，且当x∈
时，f(x)≤g(x)，求a的取值范围．
（1）{x|0＜x＜2}（2）
【解析】(1)当a＝－2时，不等式f(x)＜g(x)化为|2x－1|＋|2x－2|－x－3＜0.
设函数y＝|2x－1|＋|2x－2|－x－3，
则y＝
其图象如图所示，
由图象可知，当且仅当x∈(0,2)时，y＜0.
所以原不等式的解集是{x|0＜x＜2}．
(2)当x∈
时，f(x)＝1＋a，
不等式f(x)≤g(x)化为1＋a≤x＋3，所以x≥a－2对x∈都成立，
应有－
≥a－2，则a≤
，从而实数a的取值范围是.
练习册系列答案
相关题目
