题目内容
下列函数中,在其定义域内,既是单调递增函数,又是奇函数的是
- A.f(x)=sinx+x2
- B.f(x)=

- C.
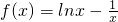
- D.f(x)=3x-3-x
D
分析:C:因为函数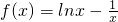 的定义域为(0,+∞)不关于原点对称,所以此函数不具有奇偶性.
的定义域为(0,+∞)不关于原点对称,所以此函数不具有奇偶性.
A:因为函数不满足f(-x)≠-f(x),所以此函数在定义域内不是奇函数.
B:由函数的解析式可得:f′(x)=1- ≥0在其定义域内不是恒成立,所以函数在定义域内不是单调递增函数.
≥0在其定义域内不是恒成立,所以函数在定义域内不是单调递增函数.
D:由题意可得f(-x)=-f(x),并且f′(x)= >0恒成立,所以此函数既是单调递增函数,又是奇函数.
>0恒成立,所以此函数既是单调递增函数,又是奇函数.
解答:根据函数奇偶性的定义可得:若函数具有奇偶性则其定义域关于原点对称,因为函数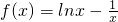 的定义域为(0,+∞),所以此函数不具有奇偶性,所以C答案错误.
的定义域为(0,+∞),所以此函数不具有奇偶性,所以C答案错误.
A:因为函数的解析式为f(x)=sinx+x2,所以f(-x)≠-f(x),所以此函数在定义域内不是奇函数,所以A错误.
B:由函数f(x)= 可得:f′(x)=1-
可得:f′(x)=1- ,所以f′(x)=1-
,所以f′(x)=1- ≥0在其定义域内不是恒成立,所以函数在定义域内不是单调递增函数,所以B错误.
≥0在其定义域内不是恒成立,所以函数在定义域内不是单调递增函数,所以B错误.
D:由函数f(x)=3x-3-x可得f(-x)=-f(x),并且f′(x)= >0恒成立,所以此函数既是单调递增函数,又是奇函数,所以D正确.
>0恒成立,所以此函数既是单调递增函数,又是奇函数,所以D正确.
故选D.
点评:本题主要考查函数的奇偶性与单调性,解决此类问题的关键是熟练掌握函数奇偶性的定义域判定方法,以及掌握利用导数判定函数的单调性,掌握导数的运算公式与运算法则.
分析:C:因为函数
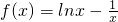 的定义域为(0,+∞)不关于原点对称,所以此函数不具有奇偶性.
的定义域为(0,+∞)不关于原点对称,所以此函数不具有奇偶性.A:因为函数不满足f(-x)≠-f(x),所以此函数在定义域内不是奇函数.
B:由函数的解析式可得:f′(x)=1-
 ≥0在其定义域内不是恒成立,所以函数在定义域内不是单调递增函数.
≥0在其定义域内不是恒成立,所以函数在定义域内不是单调递增函数.D:由题意可得f(-x)=-f(x),并且f′(x)=
 >0恒成立,所以此函数既是单调递增函数,又是奇函数.
>0恒成立,所以此函数既是单调递增函数,又是奇函数.解答:根据函数奇偶性的定义可得:若函数具有奇偶性则其定义域关于原点对称,因为函数
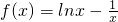 的定义域为(0,+∞),所以此函数不具有奇偶性,所以C答案错误.
的定义域为(0,+∞),所以此函数不具有奇偶性,所以C答案错误.A:因为函数的解析式为f(x)=sinx+x2,所以f(-x)≠-f(x),所以此函数在定义域内不是奇函数,所以A错误.
B:由函数f(x)=
 可得:f′(x)=1-
可得:f′(x)=1- ,所以f′(x)=1-
,所以f′(x)=1- ≥0在其定义域内不是恒成立,所以函数在定义域内不是单调递增函数,所以B错误.
≥0在其定义域内不是恒成立,所以函数在定义域内不是单调递增函数,所以B错误.D:由函数f(x)=3x-3-x可得f(-x)=-f(x),并且f′(x)=
 >0恒成立,所以此函数既是单调递增函数,又是奇函数,所以D正确.
>0恒成立,所以此函数既是单调递增函数,又是奇函数,所以D正确.故选D.
点评:本题主要考查函数的奇偶性与单调性,解决此类问题的关键是熟练掌握函数奇偶性的定义域判定方法,以及掌握利用导数判定函数的单调性,掌握导数的运算公式与运算法则.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
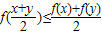 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数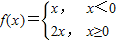
 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数