题目内容
已知函数f(x)=lnx,g(x)=﹣x2+ax.
(1)函数h(x)=f(x)﹣g(x)在其定义域内是增函数,求a的取值范围;
(2)在(1)的结论下,设φ(x)=e2x+aex,x∈[0,ln2],求函数φ(x)的最小值.
(1)函数h(x)=f(x)﹣g(x)在其定义域内是增函数,求a的取值范围;
(2)在(1)的结论下,设φ(x)=e2x+aex,x∈[0,ln2],求函数φ(x)的最小值.
解:(1)依题意:h(x)=lnx+x2﹣ax
∵h(x)在(0,+∞)上是增函数,
∴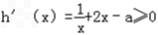 对x∈(0,+∞)恒成立,
对x∈(0,+∞)恒成立,
∴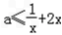 ,
,
∵x>0,则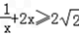 .
.
∴b的取值范围是 .
.
(2)设t=ex,则函数化为y=t2+at,t∈[1,2]
∵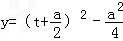
当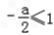 ,即
,即 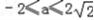 时,函数y在[1,2]上为增函数,
时,函数y在[1,2]上为增函数,
∴当t=1时,ymin=a+1;
当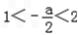 ,即﹣4<a<﹣2时,t=﹣
,即﹣4<a<﹣2时,t=﹣ ,ymin=
,ymin=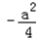 ;
;
当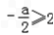 ,即a≤﹣4时,函数y在[1,2]上为减函数,
,即a≤﹣4时,函数y在[1,2]上为减函数,
∴当t=2时,ymin=2a+4.
综上所述: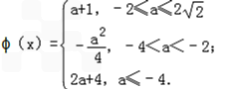
∵h(x)在(0,+∞)上是增函数,
∴
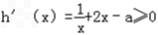 对x∈(0,+∞)恒成立,
对x∈(0,+∞)恒成立, ∴
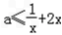 ,
, ∵x>0,则
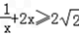 .
. ∴b的取值范围是
 .
.(2)设t=ex,则函数化为y=t2+at,t∈[1,2]
∵
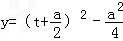
当
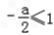 ,即
,即 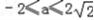 时,函数y在[1,2]上为增函数,
时,函数y在[1,2]上为增函数, ∴当t=1时,ymin=a+1;
当
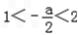 ,即﹣4<a<﹣2时,t=﹣
,即﹣4<a<﹣2时,t=﹣ ,ymin=
,ymin=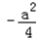 ;
;当
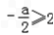 ,即a≤﹣4时,函数y在[1,2]上为减函数,
,即a≤﹣4时,函数y在[1,2]上为减函数, ∴当t=2时,ymin=2a+4.
综上所述:
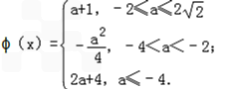

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目