题目内容
13.已知a>0,b>0,且$\frac{3}{a}$+$\frac{1}{b}$≥$\frac{m}{a+3b}$恒成立,求m的最大值.分析 利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵a>0,b>0,不等式且$\frac{3}{a}$+$\frac{1}{b}$≥$\frac{m}{a+3b}$恒成立,
∴m≤(a+3b)($\frac{3}{a}$+$\frac{1}{b}$),
∵(a+3b)($\frac{3}{a}$+$\frac{1}{b}$)=3+3+$\frac{a}{b}$+$\frac{9b}{a}$≥6+2$\sqrt{\frac{a}{b}•\frac{9b}{a}}$=12,当且仅当a=3b时取等号.
∴m的最大值等于12.
点评 本题考查了“乘1法”与基本不等式的性质、恒成立问题的等价转化方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
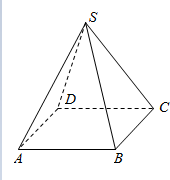 如图,在正四棱锥S-ABCD中,底面边长为6cm,侧棱长为3$\sqrt{5}$cm.
如图,在正四棱锥S-ABCD中,底面边长为6cm,侧棱长为3$\sqrt{5}$cm.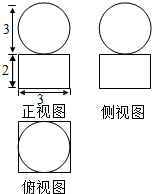 设如图是某几何体的三视图,求该几何体的体积和表面积.
设如图是某几何体的三视图,求该几何体的体积和表面积.