题目内容
已知函数f(x)=ax3+x2-ax(a,x∈R).
(1)若函数f(x)在区间(1,2)上不是单调函数,试求a的取值范围;
(2)设函数 ,如果存在a∈(-∞,-1],对任意x∈(-1,b](b>-1)都有h(x)≥0成立,试求b的最大值.
,如果存在a∈(-∞,-1],对任意x∈(-1,b](b>-1)都有h(x)≥0成立,试求b的最大值.
解:(1)由题意知,f'(x)=3ax2+2x-a在区间(1,2)内有不重复的零点…(1分)
由3ax2+2x-a=0,得a(3x2-1)=-2x…(2分)
∵3x2-1≠0,∴ …(3分)
…(3分)
令 ,
, …(4分)
…(4分)
故 在区间(1,2)上是增函数,其值域为
在区间(1,2)上是增函数,其值域为 ,
,
∴a的取值范围是 …(6分)
…(6分)
(2)∵h(x)=ax3+(3a+1)x2+(2-a)x-a,
由已知得:h(x)≥h(-1)在区间[-1,b]上恒成立,即(x+1)[ax2+(2a+1)x+(1-3a)]≥0…①…(7分)
当x=-1时,不等式①成立…(8分)
当-1<x≤b时,不等式①化为:ax2+(2a+1)x+(1-3a)≥0…②…(9分)
令φ(x)=ax2+(2a+1)x+(1-3a),由于二次函数φ(x)的图象是开口向下的抛物线,
故它在闭区间上的最小值必在区间端点处取得,又φ(-1)=-4a>0…(10分)
∴不等式②恒成立的充要条件是φ(b)≥0,即ab2+(2a+1)b+(1-3a)≥0,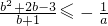 ,
,
∵这个关于a的不等式在区间(-∞,-1]上有解,
∴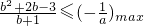 ,即
,即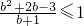 ,∴b2+b-4≤0…(11分)
,∴b2+b-4≤0…(11分)
∴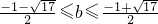 ,又b>-1,故
,又b>-1,故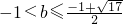 …(12分)
…(12分)
从而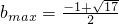 ,此时唯有a=-1符合条件…(14分)
,此时唯有a=-1符合条件…(14分)
分析:(1)由题意知,f'(x)=3ax2+2x-a在区间(1,2)内有不重复的零点,由3ax2+2x-a=0,分离参数,构造新函数,确定其值域,即可求得结论;
(2)存在a∈(-∞,-1],对任意x∈(-1,b](b>-1)都有h(x)≥0成立,等价于h(x)≥h(-1)在区间[-1,b]上恒成立,即(x+1)[ax2+(2a+1)x+(1-3a)]≥0,进而分类讨论,即可求得结论.
点评:本题考查利用导数求闭区间上函数最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想,属于中档题.
由3ax2+2x-a=0,得a(3x2-1)=-2x…(2分)
∵3x2-1≠0,∴
 …(3分)
…(3分)令
 ,
, …(4分)
…(4分)故
 在区间(1,2)上是增函数,其值域为
在区间(1,2)上是增函数,其值域为 ,
,∴a的取值范围是
 …(6分)
…(6分)(2)∵h(x)=ax3+(3a+1)x2+(2-a)x-a,
由已知得:h(x)≥h(-1)在区间[-1,b]上恒成立,即(x+1)[ax2+(2a+1)x+(1-3a)]≥0…①…(7分)
当x=-1时,不等式①成立…(8分)
当-1<x≤b时,不等式①化为:ax2+(2a+1)x+(1-3a)≥0…②…(9分)
令φ(x)=ax2+(2a+1)x+(1-3a),由于二次函数φ(x)的图象是开口向下的抛物线,
故它在闭区间上的最小值必在区间端点处取得,又φ(-1)=-4a>0…(10分)
∴不等式②恒成立的充要条件是φ(b)≥0,即ab2+(2a+1)b+(1-3a)≥0,
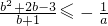 ,
,∵这个关于a的不等式在区间(-∞,-1]上有解,
∴
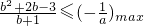 ,即
,即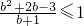 ,∴b2+b-4≤0…(11分)
,∴b2+b-4≤0…(11分)∴
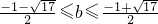 ,又b>-1,故
,又b>-1,故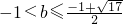 …(12分)
…(12分)从而
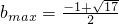 ,此时唯有a=-1符合条件…(14分)
,此时唯有a=-1符合条件…(14分)分析:(1)由题意知,f'(x)=3ax2+2x-a在区间(1,2)内有不重复的零点,由3ax2+2x-a=0,分离参数,构造新函数,确定其值域,即可求得结论;
(2)存在a∈(-∞,-1],对任意x∈(-1,b](b>-1)都有h(x)≥0成立,等价于h(x)≥h(-1)在区间[-1,b]上恒成立,即(x+1)[ax2+(2a+1)x+(1-3a)]≥0,进而分类讨论,即可求得结论.
点评:本题考查利用导数求闭区间上函数最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想,属于中档题.

练习册系列答案
相关题目