题目内容
已知等差数列{an}的前n项和为Sn,且a3=5,S15=225.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设
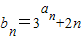 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
【答案】分析:(Ⅰ)等差数列{an}的前n项和为Sn,且a3=5,S15=225,利用等差数列的通项公式和前n项和公式列出方程组,先求出等差数列的首项和公差,由此能求了an.
(Ⅱ)由(Ⅰ)知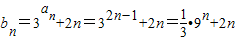 ,由此利用分组求和法能求出数列{bn}的前n项和Tn.
,由此利用分组求和法能求出数列{bn}的前n项和Tn.
解答:解:(Ⅰ)∵等差数列{an}的前n项和为Sn,且a3=5,S15=225,
∴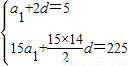 ,
,
解得 ,
,
∴an=2n-1.…(6分)
(Ⅱ)∵an=2n-1,
∴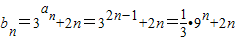 ,
,
∴Tn=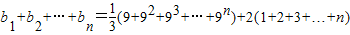
=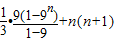
=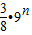 +n(n+1)
+n(n+1)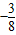 …(12分)
…(12分)
点评:本题考查数列的通项公式和前n项和的求法,解题时要认真审题,仔细解答,注意待定系数法和分组求和法的合理运用.
(Ⅱ)由(Ⅰ)知
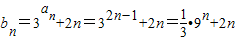 ,由此利用分组求和法能求出数列{bn}的前n项和Tn.
,由此利用分组求和法能求出数列{bn}的前n项和Tn.解答:解:(Ⅰ)∵等差数列{an}的前n项和为Sn,且a3=5,S15=225,
∴
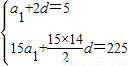 ,
,解得
 ,
,∴an=2n-1.…(6分)
(Ⅱ)∵an=2n-1,
∴
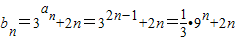 ,
,∴Tn=
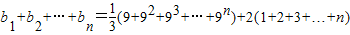
=
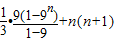
=
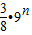 +n(n+1)
+n(n+1)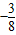 …(12分)
…(12分)点评:本题考查数列的通项公式和前n项和的求法,解题时要认真审题,仔细解答,注意待定系数法和分组求和法的合理运用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.