题目内容
设函数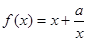 定义域为
定义域为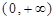 ,且
,且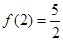 .设点
.设点 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点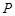 分别作直线
分别作直线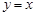 和
和  轴的垂线,垂足分别为
轴的垂线,垂足分别为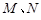 .
.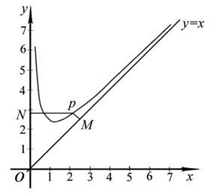
(1)写出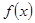 的单调递减区间(不必证明);
的单调递减区间(不必证明);
(2)问: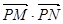 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;
(3)设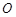 为坐标原点,求四边形
为坐标原点,求四边形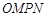 面积的最小值.
面积的最小值.
(1)函数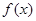 在
在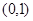 上是减函数.
上是减函数.
(2)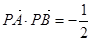
(3)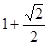 。
。
解析试题分析:
思路分析:(1)根据函数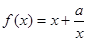 的图象过点
的图象过点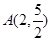 ,确定a,进一步认识函数的单调性。
,确定a,进一步认识函数的单调性。
(2)、设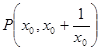 ,根据直线
,根据直线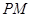 的斜率
的斜率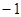 ,确定
,确定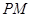 的方程。
的方程。
利用联立方程组求得M,N的坐标,计算可得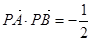 。
。
(3)、为求四边形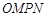 面积的最小值,根据(2)将面积用
面积的最小值,根据(2)将面积用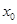 表示,
表示, 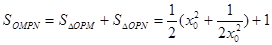 ,应用均值定理求解。
,应用均值定理求解。
解:(1)、因为函数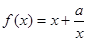 的图象过点
的图象过点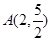 ,
,
所以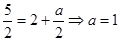 函数
函数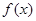 在
在 上是减函数.
上是减函数.
(2)、设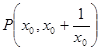 ,直线
,直线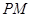 的斜率
的斜率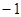 ,
,
则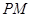 的方程
的方程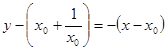 。
。
联立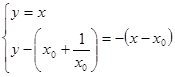 ,
,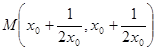 、
、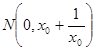
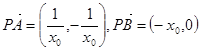 ,
,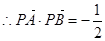
(2)、(文)设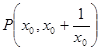 ,直线
,直线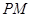 的斜率为
的斜率为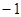 ,
,
则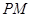 的方程
的方程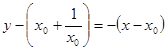 ,
,
联立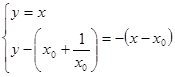 ,
,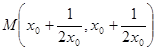 ,
,
3、 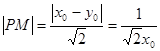 ,
,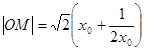 ,
,
∴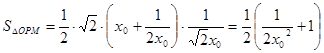 ,
,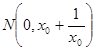 ,
,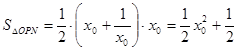 ,
,
∴ 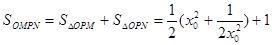 ,
,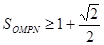 ,
,
当且仅当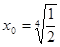 时,等号成立,∴ 此时四边形
时,等号成立,∴ 此时四边形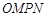 面积有最小值
面积有最小值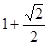 。
。
考点:函数的单调性,直线与双曲线的位置关系,平面向量的坐标运算,均值定理的应用,面积计算。
点评:中档题,本题综合性较强,难度较大。以“对号函数”为背景,综合考查函数的单调性,直线与双曲线的位置关系,平面向量的坐标运算,均值定理的应用,面积计算等。

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 (升)关于行驶速度
(升)关于行驶速度 (千米/每小时)的函数解析式可以表示为
(千米/每小时)的函数解析式可以表示为 ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.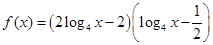 。
。 时,求该函数的值域;
时,求该函数的值域; 对于
对于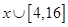 恒成立,求
恒成立,求 有取值范围。
有取值范围。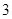 年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第
年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第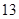 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加 直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多
直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多 元.
元. 个月还清贷款(
个月还清贷款( ),试用
),试用 表示小王第
表示小王第 )个月的还款额
)个月的还款额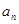 ;
; 时,小王将在第几个月还清最后一笔贷款?
时,小王将在第几个月还清最后一笔贷款? 元的基本生活费?(参考数据:
元的基本生活费?(参考数据: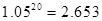 )
) 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数. 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.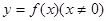 对于任意的
对于任意的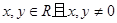 满足
满足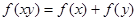 .
.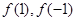 的值;
的值; 为偶函数;
为偶函数;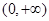 上是增函数,解不等式
上是增函数,解不等式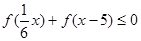
 年(
年(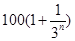 万元.设从2012年起的前
万元.设从2012年起的前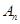 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为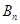 万元(须扣除开发所投入资金).
万元(须扣除开发所投入资金).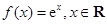 .
. 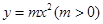 公共点的个数.
公共点的个数. 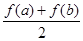 与
与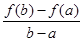 的大小, 并说明理由.
的大小, 并说明理由. 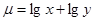 的最大值。
的最大值。