题目内容
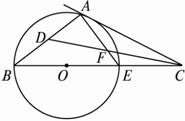
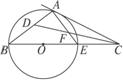
 已知C点在⊙O直径BE的延长线上,CA与⊙O切于A点,∠ACB的平分线CD交AE于点F,交AB于点D.
已知C点在⊙O直径BE的延长线上,CA与⊙O切于A点,∠ACB的平分线CD交AE于点F,交AB于点D.(1)求证:AD=AF;
(2)若AB=AC,求
| AC | BC |
分析:(1)利用等角对等边,即可得到结论;
(2)先证明△BCA∽△ACE,再确定∠CAE=∠B=∠ACB=30°,即可得到结论.
(2)先证明△BCA∽△ACE,再确定∠CAE=∠B=∠ACB=30°,即可得到结论.
解答:(1)证明:∵CA与⊙O切于A点,∴∠CAE=∠E,
又∵CD是∠ACB的平分线,∴∠ACD=∠DCB,…(2分)
∴∠ADF=∠B+∠DCB=∠CAE+∠ACD=∠AFD,…(4分)
∴AD=AF; …(5分)
(2)解:∵AB=AC,∴∠CAE=∠B=∠ACB,
又∵∠ACB=∠ACB,…(6分)
∴△BCA∽△ACE,∴
=
,…(9分)
又∵180°=∠ACE+∠CAE+∠AEC=∠ACE+∠CAE+(90°+∠ABE),
∴∠CAE=∠B=∠ACB=30°,
∴
=
=
.…(12分)
又∵CD是∠ACB的平分线,∴∠ACD=∠DCB,…(2分)
∴∠ADF=∠B+∠DCB=∠CAE+∠ACD=∠AFD,…(4分)
∴AD=AF; …(5分)
(2)解:∵AB=AC,∴∠CAE=∠B=∠ACB,
又∵∠ACB=∠ACB,…(6分)
∴△BCA∽△ACE,∴
| AC |
| BC |
| AE |
| AB |
又∵180°=∠ACE+∠CAE+∠AEC=∠ACE+∠CAE+(90°+∠ABE),
∴∠CAE=∠B=∠ACB=30°,
∴
| AC |
| BC |
| AE |
| AB |
| ||
| 3 |
点评:本题考查圆的切线的性质,考查三角形的相似,解题的关键是确定角的相等关系,属于中档题.

练习册系列答案
相关题目
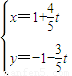 (t为参数)被曲线
(t为参数)被曲线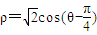 所截的弦长为 .
所截的弦长为 . (t为参数)被曲线
(t为参数)被曲线 所截的弦长为 .
所截的弦长为 .