题目内容

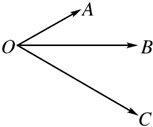如图，|
OA
|=1，|
OB
|=
3
，|
OC
|=2，∠AOB=∠BOC=30°，用
OA
，
OB
表示
OC
，则
OC
=
2
OB
-2
OA
2
OB
-2
OA
．
分析：在射线OA上取OD=2，过点D作DE∥OC交射线OB于点E，可证明
DE
=
OC
，再利用向量的线性运算即可得出．
解答：解：如图所示：过点C作CE∥OA交OB于点E，再过E作ED∥OC交OA于点D，则四边形OCED是平行四边形，
∴
DE
=
OC
，
∵DE∥OC，∴∠DEC=30°，∴∠DOE=∠OED=30°，∴OD=DE=2，∠ODE=120°．
∴＜
OD
，
DE
＞=60°．
∵
OE
=
OD
+
DE
，
∴
OE
2=(
OD
+
DE
)2=
OD
2+
DE
2+2
OD
•
DE

=22×2+2×2×2cos60°=12，∴|
OE
|=2
3
．
在△ODE中，
DE
=
OE
-
OD
，
而
OD
=2
OA
，
OE
=
OB
|
OB
|
×|
OE
|=2
OB
．
∴
OC
=2
OB
-2
OA
．
故答案为2
OB
-2
OA
点评：熟练掌握向量的线性运算法则是解题的关键．
练习册系列答案
相关题目
椭圆C1的焦点在x轴上，中心是坐标原点O，且与椭圆C2：
x2
12
+
y2
4
=1的离心率相同，长轴长是C2长轴长的一半．A（3，1）为C2上一点，OA交C1于P点，P关于x轴的对称点为Q点，过A作C2的两条互相垂直的动弦AB，AC，分别交C2于B，C两点，如图．

（1）求椭圆C1的标准方程；
（2）求Q点坐标；
（3）求证：B，Q，C三点共线．
（2012•江西）如图，|OA|=2（单位：m），OB=1（单位：m），OA与OB的夹角为
π
6
，以A为圆心，AB为半径作圆弧
BDC
与线段OA延长线交与点C．甲、乙两质点同时从点O出发，甲先以速度1（单位：m/s）沿线段OB行至点B，再以速度3（单位：m/s）沿圆弧
BDC
行至点C后停止；乙以速率2（单位：m/s）沿线段OA行至A点后停止．设t时刻甲、乙所到的两点连线与它们经过的路径所围成图形的面积为S（t）（S（0）=0），则函数y=S（t）的图象大致是（　　）
（2009•杨浦区一模）（文）已知△OAB，
OA
=
a
，
OB
=
b
，|
a
|=
2
，|
b
|=
3
，
a
•
b
=1，边AB上一点P1，这里P1异于A、B．由P1引边OB的垂线P1Q1，Q1是垂足，再由Q1引边OA的垂线Q1R1，R1是垂足．又由R1引边AB的垂线R1P2，P2是垂足．同样的操作连续进行，得到点　Pn、Qn、Rn（n∈N*）．设 
APn
=tn(
b
-
a
)(0＜tn＜1），如图．
（1）．求|
AB
|的值；
（2）．某同学对上述已知条件的研究发现如下结论：
BQ1
=-
2
3
(1-t1)
b
，问该同学这个结论是否正确？并说明理由；
（3）．当P1、P2重合时，求△P1Q1R1的面积．
（2009•杨浦区一模）已知△OAB，
OA
=
a
，
OB
=
b
，|
a
|=
2
，|
b
|=
3
，
a
•
b
=1，边AB上一点P1，这里P1异于A、B．由P1引边OB的垂线P1Q1，Q1是垂足，再由Q1引边OA的垂线Q1R1，R1是垂足．又由R1引边AB的垂线R1P2，P2是垂足．同样的操作连续进行，得到点　Pn、Qn、Rn（n∈N*）．设 
APn
=tn(
b
-
a
)(0＜tn＜1），如图．
（1）求|
AB
|的值；
（2）某同学对上述已知条件的研究发现如下结论：
BQ1
=-
2
3
(1-t1)
b
，问该同学这个结论是否正确？并说明理由；
（3）用t1和n表示tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网