Question

【题目】在直角坐标系中,以原点为极点, 轴的正半轴为极轴建立极坐标系,已知曲线:,已知过点的直线的参数方程为: (为参数),直线与曲线分别交于两点.

(1)写出曲线和直线的普通方程;

(2)若,,成等比数列,求的值.

Answer 1

【答案】(1) , x-y-2=0.

(2)1.

【解析】

（1）将曲线C的极坐标方程两边乘以得到，然后将代入可得直角坐标方程；消去直线参数方程中的参数后可得普通方程．（2）将直线的参数方程代入曲线的直角坐标方程得到关于的一元二次方程，然后结合题意及参数的几何意义求解．

(1)∵曲线的极坐标方程为，

∴．

将代入上式，

得．

∴曲线的直角坐标方程为:．

消去参数方程 (为参数)中的参数，可得，

∴直线的普通方程为.

(2)将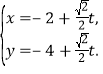 (为参数)代入整理得.

设点对应的参数分别为,，

则,,

由题意得．

∵，

∴．

∵,

∴,

∴,

解得或（舍去）．

∴．