题目内容
已知直线 与圆
与圆 交于
交于 、
、 两点,
两点, 是原点,C是圆上一点,若
是原点,C是圆上一点,若 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
C
解析试题分析:∵ 均为圆
均为圆 上的点,故
上的点,故 ,∵
,∵ ,∴
,∴ ,即
,即 ,即
,即 ,故
,故 ,则圆心
,则圆心 到直线
到直线 的距离
的距离 ,解得
,解得 .
.
考点:向量在几何中的应用;直线与圆相交的性质.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
曲线 关于( )
关于( )
A.直线 对称 对称 | B.直线 对称 对称 |
C.直线 对称 对称 | D.直线 对称 对称 |
点 在圆
在圆 的内部,则
的内部,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知圆 的圆心是直线
的圆心是直线 与
与 轴的交点,且圆
轴的交点,且圆 与直线
与直线 相切,则圆
相切,则圆 的方程是( )
的方程是( )
A. | B. |
C. | D. |
圆 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.外离 | B.相交 | C.内切 | D.外切 |
直线 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.无法确定 |
已知圆心(a,b)(a<0,b<0)在直线y=2x+1上的圆,其圆心到x轴的距离恰好等于圆的半径,在y轴上截得的弦长为2 ,则圆的方程为( )
,则圆的方程为( )
| A.(x+2)2+(y+3)2=9 | B.(x+3)2+(y+5)2=25 |
C.(x+6)2+ 2= 2= | D. 2+ 2+ 2= 2= |

 的左焦点
的左焦点 ,作圆
,作圆 的切线,切点为
的切线,切点为 ,延长
,延长 交双曲线右支于点
交双曲线右支于点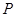 ,若
,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) 




