题目内容
函数y=1n
与函数y=cosπx图象所有交点的横坐标之和为( )
| 1 |
| |x-1| |
| A、3 | B、4 | C、6 | D、8 |
分析:把函数y=ln(
)与函数y=cosπx图象都向左平移1个单位得y=ln
=-ln|x|与y=cosπ(x+1)=-cosπx的图象(均为偶函数),在同一坐标系中作出其图形,分析可得答案.
| 1 |
| |x-1| |
| 1 |
| |x| |
解答:解:把函数y=ln(
)与函数y=cosπx图象都向左平移1个单位得y=ln
=-ln|x|与y=cosπ(x+1)=-cosπx的图象,
上述两个函数都是偶函数,其图象关于y轴对称,
在同一坐标系中作出y=-ln|x|与y=-cosπx的图象,
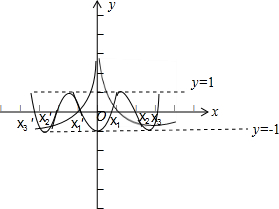
由图知,两个函数图象恰有6个交点,其横坐标分别为x1,x2,x3,与x1′,x2′,x3′,
则所有交点的横坐标之和是0;
∴函数y=ln(
)与函数y=cosπx图象也有6个交点,其横坐标分别为x1+1,x2+1,x3=1,与x1′=1,x2′+1,x3′+1,
∵(x1+x1′)+(x2+x2′)+(x3+x3′)=0,
∴(x1+1+x1′+1)+(x2+1+x2′+1)+(x3+1+x3′+1)=6,
即原来两个函数图象所有交点的横坐标之和是6.
故选:C.
| 1 |
| |x-1| |
| 1 |
| |x| |
上述两个函数都是偶函数,其图象关于y轴对称,
在同一坐标系中作出y=-ln|x|与y=-cosπx的图象,
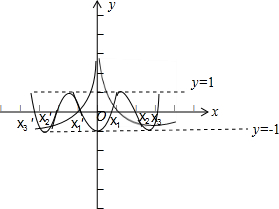
由图知,两个函数图象恰有6个交点,其横坐标分别为x1,x2,x3,与x1′,x2′,x3′,
则所有交点的横坐标之和是0;
∴函数y=ln(
| 1 |
| |x-1| |
∵(x1+x1′)+(x2+x2′)+(x3+x3′)=0,
∴(x1+1+x1′+1)+(x2+1+x2′+1)+(x3+1+x3′+1)=6,
即原来两个函数图象所有交点的横坐标之和是6.
故选:C.
点评:本题他考查对数函数与余弦函数的图象与性质,着重考查作图与分析、解决问题的能力,作图是难点,分析结论是关键,属于难题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目