题目内容
16.已知A、B、C是平面上不共线的三点,O是三角形ABC的重心,动点P满足$\overrightarrow{OP}$=$\frac{1}{3}$($\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{2}\overrightarrow{OB}$+2$\overrightarrow{OC}$),则点P一定为三角形ABC的( )| A. | 重心 | B. | AB边的中点 | ||
| C. | AB边中线的中点 | D. | AB边中线的三等分点(非重心) |
分析 根据题意,画出图形,结合图形,利用向量加法的平行四边形法则以及共线的向量的加法法则,即可得出正确的结论.
解答 解:如图所示,
设AB 的中点是E,
∵O是三角形ABC的重心,
∴$\overrightarrow{OP}$=$\frac{1}{3}$($\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$+2$\overrightarrow{OC}$)=$\frac{1}{3}$($\overrightarrow{OE}$+2$\overrightarrow{OC}$);
又∵$\overrightarrow{OC}$=2$\overrightarrow{EO}$,
∴$\overrightarrow{OP}$=$\frac{1}{3}$($\overrightarrow{OE}$+4$\overrightarrow{EO}$)=$\overrightarrow{EO}$;
∴点P在AB边的中线CE上,是中线CE的三等分点,但不是重心O.
故选:D.
点评 本题考查了平面向量的应用问题,也考查了三角形的重心的应用问题,是综合性题目.

练习册系列答案
相关题目
6.过点P(-2,2)作直线l,使直线l与两坐标轴在第二象限内围成的三角形面积为8,这样的直线l一共有( )
| A. | 3条 | B. | 2条 | C. | 1条 | D. | 0条 |
11.设a=$\frac{200{7}^{\frac{1}{n}}-200{7}^{-\frac{1}{n}}}{2}$(n∈N*),那么($\sqrt{1+{a}^{2}}$-a)n的结果是( )
| A. | 2007-1 | B. | -2007-1 | C. | (-1)n•2007 | D. | (-1)n•2007-1 |
6.下列命题中正确的是( )
| A. | 命题“?x∈R,x2-x≤0”的否定是“?x∈R,x2-x≥0” | |
| B. | 命题“p∧q为真”是命题“p∨q为真”的必要不充分条件 | |
| C. | 若“am2≤bm2,则a≤b”的否命题为真 | |
| D. | 若实数x,y∈[-1,1],则点(x,y)所构成的平面区域为π |
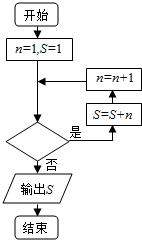 已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.
已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.