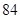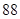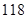题目内容
设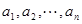 是1,2,…,
是1,2,…,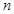 的一个排列,把排在
的一个排列,把排在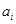 的左边且比
的左边且比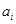 小的数的个数称为
小的数的个数称为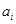 的顺序数(
的顺序数(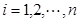 )。如:在排列
)。如:在排列 中,5的顺序数为1,3的顺序数为0。则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列种数为( )
中,5的顺序数为1,3的顺序数为0。则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列种数为( )
| A.48 | B.96 | C.144 | D.192 |
C
解析试题分析:由于8是最大的数,8的顺序数为2,说明8排在第3位,如下所示
(),(),8,(),(),(),(),()
7仅次于8,且7的顺序数为3,所以7只能排在第5位,如下所示
(),(),8,(),7,(),(),()
5的顺序数为3,但是还有一个比5大的6的位置没有确定
假如6排在5的右边,那么排在第一,二,四位的3个数肯定比5小,所以5排在第6位
(),(),8,(),7,5,(),()
在这种情况下6可以排在第七或第八的位置,剩下的数可以全排列插入剩下的空中,
所以种数为 2 4!=48
4!=48
假如6排在5的右边,那么5排在第七位
(),(),8,(),7,(),5,()
在这种情况下6可以排在第一,二,四,六的位置,剩下的数可以全排列插入剩下的空中,
所以种数为 4 4!=96,所以总数为48+96=144
4!=96,所以总数为48+96=144
考点:本试题考查了排列组合的运用。
点评:对于比较复杂的排列组合试题,一般要合理的分情况来讨论,进而结合分步乘法计数原理来得到各种情况下的结果,然后根据分类加法计数原理得到最终的结论,属于难度试题。另解就是:在确定7,8的位置以后 (),(),8,(),7,(),(),(),由于6没有限制,随便填入有6种可能,当6填入以后,5的位置也唯一确定了,剩下的4个数全排列,所以是 6 4!=144
4!=144

将4个不同的球放入3个不同的盒中,每个盒内至少有1个球,则不同的放法种数为( )
| A.24 | B.36 | C.48 | D.96 |
某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在第四位、节目乙不能排在第一位,节目丙不能排在最后一位,该台晚会节目演出顺序的编排方案共有
| A.36种 | B.42种 | C.48种 | D.54种 |
 展开式中的常数项是
展开式中的常数项是
A. | B. | C. | D. |
在二项式 的展开式中,各项系数之和为A,各项二项式系数之和为B,且
的展开式中,各项系数之和为A,各项二项式系数之和为B,且 ,则展开式中常数项的值为 ( )
,则展开式中常数项的值为 ( )
| A.6 | B.9 | C.12 | D.18 |
 的展开式中
的展开式中 的项的系数是( )
的项的系数是( )
A. | B. | C. | D. |
 且
且 ,则乘积
,则乘积 等于
等于
A. | B. | C. | D. |
已知关于x的二项式 展开式的二项式系数之和为32,常数项为80,则a的值为( )
展开式的二项式系数之和为32,常数项为80,则a的值为( )
| A.1 | B. | C.2 | D. |