Question

房屋的天花板上点P处有一光源，P在地面上的射影为Q，在地面上放置正棱锥S-ABCD，底面ABCD接触地面，已知正四棱锥S-ABCD的高为1米，底面ABCD的边长为

1

2

米，Q与正方形ABCD的中心O的距离为3米，又PQ长为3米，则棱锥影子（不包括底面ABCD）的面积的最大值为

 

．（注：正四棱锥为底面是正方形，且顶点在底面的射影是底面的中心的棱锥）

Answer 1

分析：欲使得棱锥影子（不包括底面ABCD）的面积的最大，则点C在直线OQ上，作出图形．利用相似三角形求出影子的高RQ，最后利用三角形的面积公式计算棱锥影子（不包括底面ABCD）的面积即可．

解答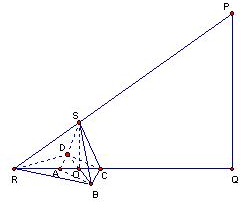：解：欲使得棱锥影子（不包括底面ABCD）的面积的最大，则点C在直线OQ上，如图．
设影子RQ=x，根据△RSO∽△RPQ，得

RO

RQ

=

SO

PQ

即

x

x+3

=

1

3

，∴x=

3

2

，
∴棱锥影子（不包括底面ABCD）的面积=S_△RBD-S_△ABD=

1

2

×

2

2

×

3

2

-

1

2

×

2

2

×

2

4

=

3 2 -1

8

．
故答案为：

3 2 -1

8

．

点评：本小题主要考查中心投影及中心投影作图法、棱柱、棱锥、棱台的侧面积和表面积等基础知识，考查运算求解能力，考查空间想象能力、化归与转化思想．属于中档题．