Question

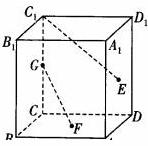
E、F、G分别是正方体BD₁的棱AA₁、CC₁、C₁D₁的中点，试作出FG与对角线BD₁所成的角,并求出FG与BE所成的角.

 

Answer 1

解析:如图,连结D₁C.由已知可知FG是△C₁D₁C的中位线，

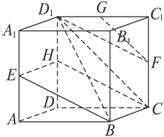
∴FG∥CD₁.

在△CD₁B中，

∵CD₁=BC＞BC,

∴∠CD₁B＜90°.

故∠CD₁B就是FG与BD₁所成的角.

取DD₁的中点H，连结CH、FD₁、EH，

∵BCAD,ADEH,

∴BCEH,BECH.

 又FCD₁H，∴FD₁CH，FD₁BE.

同上法可知∠GFD₁＜90°,故∠GFD₁是异面直线GF与BE所成的角.

在△GFD₁中可得FG=C₁D₁，D₁G=C₁D₁，FD₁=C₁D₁，

∴cos∠GFD₁=.

∴GF与BE所成角等于arccos.

小结:求异面直线所成角必须先定后算，即先确定这个角方能进行计算，而确定角时除了依据定义在适当的位置作平行线外，还应判断它是否在（0，90°］内，当求这个角的余弦值时，若为非负则是异面直线所成的角，若余弦值是负数，则异面直线所成的角应是这个角的补角.