题目内容
选做题(不等式选讲)对于任意的实数a(a≠0)和b,不等式|a+b|+|a-b|≥|a|(|x-1|+|x-2|)恒成立,试求实数x的取值范围.
解:依题意,|x-1|+|x-2|≤
恒成立,
故|x-1|+|x-2|≤(
)min.
∵|a+b|+|a-b|≥|(a+b)+(a-b)|=2|a|,当且仅当(a+b)(a-b)≥0时取“=”,
∴(
)min=2.∴x的范围即为|x-1|+|x-2|≤2的解.
解上述不等式得
≤x≤
,它就是所求的x的取值范围.
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
附加题：（选做题：在下面A、B、C、D四个小题中只能选做两题）
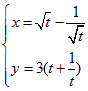的逆矩阵。
（
为参数，
），求曲线C的普通方程。
≥
＞0，求证：
≥
。
的逆矩阵。
（
为参数，
），求曲线C的普通方程。
≥
＞0，求证：
≥
。