题目内容
 在平行四边形ABCD中,设边AB、BC、CD的中点分别为E、F、G,设DF与AG、EG的交点分别为H、K,设
在平行四边形ABCD中,设边AB、BC、CD的中点分别为E、F、G,设DF与AG、EG的交点分别为H、K,设 =
= ,
, =
= ,试用
,试用 、
、 表示
表示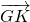 、
、 .
.
 解:如图所示,因为AB、BC、CD的中点分别为E、F、G,
解:如图所示,因为AB、BC、CD的中点分别为E、F、G,所以
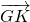 =
= +
+
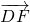 =
= +
+ (
(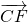 -
- )
)=-

 +
+ (-
(-
 +
+ )=-
)=-

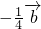 .(5分)
.(5分)因为A、H、G三点共线,
所以存在实数m,使
 =m
=m =m(
=m( +
+
 )=m
)=m +
+ m
m ;
;又D、H、F三点共线,
所以存在实数n,使
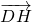 =n
=n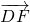 =n(
=n( -
- )=n
)=n -
- n
n .
.因为
 +
+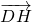 =
= ,所以
,所以 +n
+n =m
=m +
+
 (10分)
(10分)因为a、b不共线,
∴
 解得m=
解得m= ,
,即
 =
= (
( +
+ )=
)=
 +
+
 .(14分)
.(14分)分析:本题是向量伯一道综合题,需要综合运用平面向量的加减法与向量的数乘运算来达到用两个基向量
 、
、 表示
表示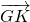 、
、 的目的,所研究的两个向量与两个基向量不在一个三角形中,故需要先用根据图形用与它们共线的向量将它们表示出来,然后再用两个基向量表示.
的目的,所研究的两个向量与两个基向量不在一个三角形中,故需要先用根据图形用与它们共线的向量将它们表示出来,然后再用两个基向量表示.点评:本题考点是向量数乘的运算及其几何意义,考查了向量的三角形法则与向量数乘的几何意义,本题是向量的运算法则的综合运用,要注意结合图形依据向量的相关的知识进行正确转化,当画图时必画图.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).
如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).