题目内容
下列命题中,真命题是( )A.若{an}是等差数列,则{|an|}也是等差数列
B.若{|an|}是等差数列,则{an}也是等差数列
C.若存在n∈N*,使2an+1=an+an+1,则{an}是等差数列
D.若{an}是等差数列,则对任意n∈N*,都有2an+1=an+an+2
解析:A.如-2,-1,0,1,2,…成等差数列,但|-2|,|-1|,0,1,2,…并不成等差数列.故A选项不正确.B.如|-3|,4,5,6,…成等差数列,但-3,4,5,6,…并不成等差数列.故选项B不正确.C.若存在某一个n∈N*,使2an+1=an+an+1,即an+1=an成立,{an}不一定是等差数列.只有对所有的n∈N*使得2an+1=an+an+1成立,{an}才是等差数列.D.由等比数列的性质可知,当n∈N*时都有2an+1=an+an+2成立时,{an}是等差数列.故选项D正确.∴应选D.
答案:D

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
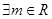 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1